全国公立高校入試
　１番問題　【令和７年春】
（２６）京都府 　学習日　　　 月　　 　日（　　　）
印刷して、紙の上でやってネ！ 　印刷用
前　　　　　　　　期
１
　1－82÷( )2



　		 ７ 　2次方程式 x2ー(a＋2)x＋2a＋5＝0 の解の1つがー3であるとき,aの値ともう1つの解をそれぞれ求めよ









　
２
　18( x＋ )－4(5－x)



　　　  
３ (2√7＋2)(2√7－2)


　		 ８ 　関数y＝9x2 について,xの変域がp≦x≦－のときのyの変域が≦y≦1である。このときのpの値を求めよ。








　
４ 　次のア～エを,絶対値の小さいものから順に並べかえ,記号で書け。

　　ア 3　 　イ －　　ウ －2.9 　　工 0

　
５ 　方程式 5x－3y＝3x＋7＝－5y＋8 解け。







　		 ９
階級(分) 累積度数(人)
以上未満
0～10
4
10～20 9
20～30 16
30～40 22
40～50 27
50～60 30
　右の表は,ある中学校で生徒30人のある日の読書時間を調査し,その結果について,累積度数をまとめたものである。この表から読み取れる読書時間の最頻値を求めよ。











　
６ 　内角の和が5040°である正多角形の1つの内角の大きさを求めよ。




　

中　　　　　　　　期
１
　11－( －1)×(－2)2




　		 ６ 　ax2－5ax－24a を因数分解せよ。




　
２
　5x－1 － －x＋2
　6 12




　		 ７ 　図は,グラフ作成ソフトウェアで4つの関数のグラフを表示させた,コンピュータの画面を表したものであり,ア～エはそれぞれ,
　　関数y＝x2, y＝ x2, y＝－7x2, y＝－ x2
のグラフのいずれかである。
　図中のア～エのうち,関数y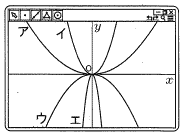＝－x2のグラフにあたるものとして最も適当なものを1つ選べ。



　　　　　　






　
３ 　(8－√8)(1＋√8)





　
４ 　半径9cm,弧の長さ10πcmのおうぎ形の中心角の大きさを求めよ。





　
５ 　次の連立方程式を解け。
　 x＝－9y－3
x＝3y＋3









　		 ８ 　次の資料は,ある中学校の3年生9人の反復横とびの記録をまとめたものである。この資料について,3年生の記録の四分位範囲を求めよ。

　資料　3年生9人の反復横とびの記録
　52， 41， 48， 57， 45， 35， 50， 56， 43　(点)







　

［トップに戻る］ ［前ページに戻る］　［次ペ－ジに進む］ ［答のペ－ジに進む］　やさしい　ややむずかしい