|
正 答 4 | |||
| 25 滋賀県 〜 32 島根県 |
|
正 答 4 | |||
| 25 滋賀県 〜 32 島根県 |
| 25滋賀県 | 1 6−5=1
よって, y=2a−x (y=−x+2aも可) 4 上式を下式に代入すると,3x+2(2x+4)=1 これを解いて, x=−1, y=2 5 (x+6)(x−4)=0より, x=−6,4 6 3×2−6√2+2√2−4=2−4√2 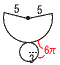 7 (右図参照) 7 (右図参照)側面の扇形の弧=底面の円周=6πcm 側面積= 8 (右表参照)
9 最頻値=(22+26)÷2=24m 中央値は13人目で, 18m以上22m未満の階級 |
28兵庫県 | 1 12 2 −4x 3 4√2+3√2=7√24 (2x−1)2=0より, x= 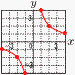 5 (右図参照) 6個 5 (右図参照) 6個
7 ∠A=96−44=52° よって,∠x=∠A=52° 8 白玉をx個とすると,
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 26京都府 | 【 前期 】
3 4×7−4=24 4 エ ウ ア イ 中辺=右辺より,3x+5y=1…ア
イより,5x+2y=8…エ ウ×2+エ×3より,19x=38で,x=2 これをエに代入して,5×2+2y=8より,y=−1 よって, x=2,y=−1 6 5040÷180=28(三角形28個分)で30角形 1つの内角=5040÷30=168° 7 元の式にx=−3を代入すると, 9+3(a+2)+2a+5=0 5a+20=0より, a=−4 元の式にa=−4を代入して,x2+2x−3=0 (x+3)(x−1)=0より,もう1つの解はx=1 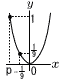 8 (右図参照) 8 (右図参照)x=pのとき,y=1となるから, 1=9p2で,p<− 9 各度数を計算すると, 4 5 7 6 5 3 となる 最頻値は20〜30の階級で, 25分 【 中期 】 1 11+
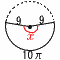 3 8+7√8−8=7√8=14√2 3 8+7√8−8=7√8=14√24 (右図参照)
これを下式に代入して,1=3y+3より,y=− よって, x=3, y=− 6 a(x2−5x−24)=a(x−8)(x+3) 7 ウ (上に凸で,大きく開いている) 8 並べかえると, 35 41 | 43 45 48 50 52 | 56 57 四分位範囲=Q3―Q1=54−42=12点 |
29奈良県 |
2 上式×3+下式より,20x=40で,x=2 これを上式に代入して,12−y=13で,y=−1 よって, x=2, y=−1 3 2乗して,6.25<a<16より, 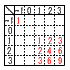 a=7,8,…,15で, 9個 a=7,8,…,15で, 9個4 0.7x×0.9=0.63x円 5 (右図参照) 10通りだから,確率=10/25= 6 102°の外角=78° 外角の和=x+62+78+65+85=360より, 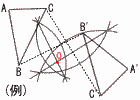 ∠x=360−290=70° ∠x=360−290=70°7 右図 (例) 対応する点を結ぶ線分の 垂直二等分線の交点Oをとる 8 エ Q2(8番目)=100〜105g Q1(4番目)=90〜95g Q3(12番目)=105〜110g |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 30和歌山県 |
2 (x+6)(x−1)=0より, x=−6,1 3 ウ,オ (エ −√16=−4で,有理数) 4 y=axに(4,6)を代入すると,
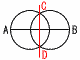 5 (右図参照) 垂直二等分線 5 (右図参照) 垂直二等分線6 およそx人とすると,比率より,
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 27大阪府 | 【 A 】 1 6+7=13
4 2x+2y+x−13y=3x−11y 5 28x3 6 5√5−2√5=3√5 2番問題の一部 〜おまけ〜 1 6×4+5=29 2 イ (エ √9=3で,有理数) 3 外項の積=内項の積だから, 4x=40より,x=10 4 ウ (y=1500/x)
【 B 】 1 −6−9=−15 2 20a+8b−14a−7b=6a+b
5 (2√7)2−(√2)2=28−2=26 2番問題の一部 〜おまけ〜 1 42−3×(−5)=16+15=31 2 (x+7)(x−6)=0より, x=−7,6 3 √9<n<√18だから, n=10,11,…,17で, 8個
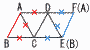 5 (右図参照) ABとFEは一致 ねじれの位置…平行でない,交わらない ABと交わるから×…AD,AC,BC FEと交わるから×…DF,DE,CE よって辺CDのみで, ア |
31鳥取県 |
3与式=2(x2−9)=2(x+3)(x−3) 4 下式−上式×3より ,y=−3 これを上式に代入して,x−3=2で,x=5 ゆえに, x=5,y=−3 5 解の公式より,
ア…関数でない(×) イ…y=7x(〇) ウ…y=x2(×) エ…y=−x+300(〇)
8 半径3cmの半球= 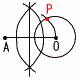 9 右図(AOを直径とする円Mと円Oの交点) 9 右図(AOを直径とする円Mと円Oの交点)・AOの垂直二等分線を引く ・中点Mを中心に,半径AMの円Mをかく ・円Mと円Oの交点をPとする 10 (1) ア 62=36通り イ (1,1) (2,2)…(6,6) (1,6) (6,1) の8通りで,8/36= (2) ウ 例 和が5か10 エ(1,4) (2,3) (4,6) が各2通りと(5,5)の7通りで, 7/36 |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 32島根県 | 1 5−6=−1 2 24ab2÷12ab=2b 3 下式−上式×2より,3y=6で,y=2 これを上式に代入して,x−8=1で,x=9 よって, x=9,y=2
5 合同条件を満たさないもの… イ ア 3辺相等 イ 2辺夾角相等 ウ 1辺両端角相等 6 (1) よって,∠x=360−210=150°
(2) 2n2>1000より, n>10√5(約22..3) よって, n=23 [別解] n2>500に当てはまる数を探す ・222=484<500 232=529>500 8 アルミ缶をx個とすると,
|
| [トップに戻る] [前ページに戻る] [次ペ−ジに進む] |