| 1 |
(1) |
 3×(-4) 3×(-4)
|
7 |
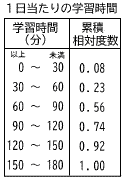 右の表は,あるクラスの生徒全員の1日当たりの学習時間について,最小の階級からの累積相対度数を示したものである。次のア~エのうち,この表から正しいと判断できるものをすべて選び,記号で答えなさい。 右の表は,あるクラスの生徒全員の1日当たりの学習時間について,最小の階級からの累積相対度数を示したものである。次のア~エのうち,この表から正しいと判断できるものをすべて選び,記号で答えなさい。
ア
|
1日当たりの学習時間が60分未満の生徒数は,このクラス全体の2割を超えている。 |
イ
|
1日当たりの学習時間が90分以上の生徒数は,このクラス全体の半数を超えている。 |
ウ
|
このクラスの中で1日当たりの学習時間が最も長い生徒は,120分以上150分未満の階級にいる。 |
エ
|
生徒数が最も多い階級は, 60分以上90分未満の階級である。 |
|
| (2) |
 (3a+5b)-(-a+b) (3a+5b)-(-a+b)
|
| (3) |
 √18-√2 √18-√2
|
| 2 |
 (x-3y)2 を展開しなさい。 (x-3y)2 を展開しなさい。
|
| 3 |
1本の値段がa円のボールペンを5本と,1個の値段がb円の修正テープを3個買ったところ,合計金額がちょうど2000円であった。この関係を,等式で表しなさい。
|
| 4 |
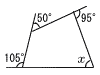 右の図の四角形において,∠xの大きさを求めなさい。 右の図の四角形において,∠xの大きさを求めなさい。
|
| 5 |
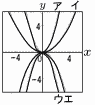 右の図のア~エの放物線は,関数y=-x2, y=- 右の図のア~エの放物線は,関数y=-x2, y=-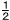 x2,y= x2,y=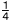 x2, y=x2のいずれかのグラフである。関数y=-x2のグラフを図のア~エから選び,記号で答えなさい。 x2, y=x2のいずれかのグラフである。関数y=-x2のグラフを図のア~エから選び,記号で答えなさい。
|
8 |
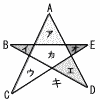  次の図において,星型の図形ABCDEの3つの頂点A,B,Cからの距離が等しい点は,この平面上に色を分けて示したア~キのうちどの部分にあるか,コンパスと定規を用いて作図して確かめ,記号で答えなさい。 次の図において,星型の図形ABCDEの3つの頂点A,B,Cからの距離が等しい点は,この平面上に色を分けて示したア~キのうちどの部分にあるか,コンパスと定規を用いて作図して確かめ,記号で答えなさい。
ただし,キは,ア~力以外の部分を示すものとする。
|
| 6 |
次の【ことがら】は,いつでも成り立つとは限らない。この【ことがら】の反例となる,∠Bの大きさと∠Cの大きさの組み合わせを,1組あげなさい。
【ことがら】
三角形ABCにおいて,∠A=60°ならば,この三角形ABCは正三角形である。 |
∠B= , ∠C=
|
9 |
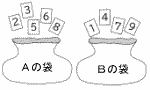 次の図のように,Aの袋には,2,3,5,6が書かれた5枚のカードを入れ,Bの袋には,1,4,7,9が書かれた4枚のカードを入れる。それぞれの袋の中をよくかき混ぜた後,それぞれの袋から1枚ずつカードを取り出して,カードに書かれた数を比べる。このとき,Aの袋から取り出したカードの数の方が大きくなる確率を求めなさい。 次の図のように,Aの袋には,2,3,5,6が書かれた5枚のカードを入れ,Bの袋には,1,4,7,9が書かれた4枚のカードを入れる。それぞれの袋の中をよくかき混ぜた後,それぞれの袋から1枚ずつカードを取り出して,カードに書かれた数を比べる。このとき,Aの袋から取り出したカードの数の方が大きくなる確率を求めなさい。
|
 右の表は,あるクラスの生徒全員の1日当たりの学習時間について,最小の階級からの累積相対度数を示したものである。次のア~エのうち,この表から正しいと判断できるものをすべて選び,記号で答えなさい。
右の表は,あるクラスの生徒全員の1日当たりの学習時間について,最小の階級からの累積相対度数を示したものである。次のア~エのうち,この表から正しいと判断できるものをすべて選び,記号で答えなさい。 右の図の四角形において,∠xの大きさを求めなさい。
右の図の四角形において,∠xの大きさを求めなさい。 右の図のア~エの放物線は,関数y=-x2, y=-
右の図のア~エの放物線は,関数y=-x2, y=-
 次の図のように,Aの袋には,2,3,5,6が書かれた5枚のカードを入れ,Bの袋には,1,4,7,9が書かれた4枚のカードを入れる。それぞれの袋の中をよくかき混ぜた後,それぞれの袋から1枚ずつカードを取り出して,カードに書かれた数を比べる。このとき,Aの袋から取り出したカードの数の方が大きくなる確率を求めなさい。
次の図のように,Aの袋には,2,3,5,6が書かれた5枚のカードを入れ,Bの袋には,1,4,7,9が書かれた4枚のカードを入れる。それぞれの袋の中をよくかき混ぜた後,それぞれの袋から1枚ずつカードを取り出して,カードに書かれた数を比べる。このとき,Aの袋から取り出したカードの数の方が大きくなる確率を求めなさい。