|
���@���@�Q | |||
| �X�@�Ȗ،��@�`�@16�@�x�R�� |
|
���@���@�Q | |||
| �X�@�Ȗ،��@�`�@16�@�x�R�� |
| �X�Ȗ،� | �P �|7 �Q 2025��81�~25��34�~52 �R (x�{5)(x�|3) �S ���������ɕ��ׂ�����, 7, 11, 16,�b 19, 20, 24 �@Q3�|Q1��20�|11��9�_ �T 8�̎O�p�`�ɕ����ł��邩��, �@���p�a��180�~8��1440�� �@1�̓��p��1440��10��144�� [�ʉ�]�O�p�̘a��360�� 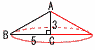 �@1�̊O�p��360��10��36��������, �@1�̊O�p��360��10��36��������,�@1�̓��p��180�|36��144�� �U (�E��}�Q��) �@�~���� 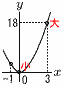 �V (�E�}�Q��) �V (�E�}�Q��)�@x���|�P�̂Ƃ�,y��2�~(�|1)2��2 �@x��3�̂Ƃ�,y��2�~32��18 �@�����, 0��y��18 �W �X����y�ؕЂ̑召���, �@a��c��0, 0��d��b��, �E �@�`�Q�Ԗ�� �i���܂��j �P ��16����23����25���, 4����23��5 �@4�ȉ��̎��R����, 1,2,3,4 �� 4��
�@�A�~3�@�|)6x�{15y��228 �@�@�@�@�@�@�@�@�@�@�@y��12 �c�E �@�E���A�ɑ������,2x�{5�~12��76��,x��8 �@�����,�Z�b�gA��8, �Z�b�gB��12 |
13�����s | �P 3�|36��4��3�|9���|6
�S ���Ӂ~2���,9x�|6��8x�{2 �@x��2�{6��8 �T �������㎮�ɑ������, �@8x�|5(2x�|1)���|3 �@8x�|10x���|3�|5 �@�|2x���|8���,x��4 �@����������ɑ������,y��2�~4�|1��7 �@�����,x��4,y��7 �U ���̌������,
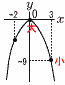 �V (�E�}�Q��) �V (�E�}�Q��)�@x��3�̂Ƃ�,y���|32���|9 �@x��0�̂Ƃ�,y���|02��0 �@�|9��y��0��, �@�A�@�A�I �W �a��10�ȏ�� �@(1,4,5) (2,3,5) (2,4,5) (3,4,5) ��4�ʂ� �@3���̎��o������,5�~4�~3��6��10�ʂ� 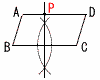 �@�����,�m����4��10�� �@�����,�m����4��10���X �E�} �E��BC�̐������������� �E��AD�Ƃ̌�_��P�Ƃ��� |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 10�Q�n�� | �P (1) �|12 �@(2) 3a�{5b�{a�|b��3a�{4b �@(3) 3��2�|��2��2��2 �Q x2�|6xy�{9y2 �R 5a�{3b��2000 �S �O�p�̘a��360��������, �@105�{50�{95�{(180�|x)��360 �@250�{180�|x��360���, ��x��70�� �T �E �@�A y��x2�@�C y�� �U ��B�{��C��120�ł���悢����, �@��B��70��,��C��50���Ȃ� 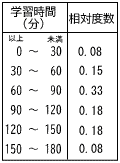 �V (�E�\�Q��)�@�A,�G �V (�E�\�Q��)�@�A,�G�@�A (�Z) 0�`60��,23�� �@�C (�~) 90�`180��,44�� �@�E (�~) �Œ���60�`90 �@�G (�Z) 60�`90��33�� �W (���}�Q��)�@�G �@�������̓_�́�ABC�̊O�S 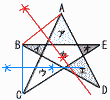
�X (�E�\�Q��)
�@ |
14�_�ސ쌧 | �A �|15 �i��1�j
�@�`�Q�Ԗ�� �i���܂��j�` �A x�|5��A�Ƃ�����, �@�^����A2�|7A�|18��(A�|9)(A�{2) �@�@��(x�|5�|9)(x�|5�{2)��(x�|14)(x�|3) �i��2�j �C ���̌������,
�@x���|1�̂Ƃ�,y���|4�~(�|1)2���|4
�@1.1x�{x��567 �@2.1x��567���,x��567��2.1��270 �@270�~1.1��297�� �i��4�j �I 2�悵��,16��n��25��,n��17,18,�c,24 �@2n���������ƂȂ�̂�,n��18�̂Ƃ� �i��2�j 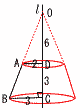 �J (�E�}�Q��) �~������ �J (�E�}�Q��) �~�������@��OAD�䁢OBC�i������2:3�j �@�@OD��x�Ƃ����,x:(x�{3)��2:3 �@�@3x��2(x�{3)���,x��OD��6 �@�~�����䁁��~�����|���~���� �@�@�� �@�@��27���|8��19�� cm3 �i��3�j |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 11��ʌ� | �P 3x�@�@�Q 10�|6��4
�@5x���|20��, x���|4
�V �����~3�|�㎮�~5���, �@29y���|58��,y���|2 �@������㎮�ɑ������, �@�@3x�{14��5��,x���|3 �����, x���|3,y���|2 �W ���̌������,
�@��DBP��,��x��57�|22��35�� 11�@�E �@45�C48�C48�C52�C54�C54�C56�C60�C62�C65�C66�C �@68�C70�C72�C74�C74�C78�C80�C84�C86�C90 �@�@Q1��54�@Q2(�����l)��66�@Q3��76 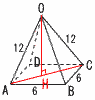 12 (�E�}�Q��)
12 (�E�}�Q��) �@AH��3��2 �@��OAH��,OH����(122�|(3��2)2 �@�@����144�|18����126��3��14 �@�̐ρ� 13 (�E�\�Q��) �@�m����8/20�� 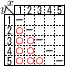 14 (�E���}�Q��) 14 (�E���}�Q��)�@��OBH��,x2�{x2��4���,x��2��2 �@��`�|��OAB��42���~ �@�@��2���|4��2 (����2) 15 �A��2����,x, x�{1�Ƃ����, 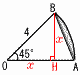 �@x2�{(x�{1)2��365 �@x2�{(x�{1)2��365�@2(x2�{x�|182)��2(x�{14)(x�|13)��0 �@x��0������,x��13�@�@�����,13��14 16 �A��21��60��0.35 (��) 54��ȏ�̊K���ɂ����鑊�Γx���̍��v��A���w�Z��0.8,B���w�Z��0.55�ł��邩��,�������傫���̂͂`���w�Z�ł���B |
15�V���� | �P �|9 �Q 15a�|10b�|8a�{4b��7a�|6b �R �|6b�~(�|3b)��18b2 �S (��10)2�|2��10��2�{(��5)2��10�|2��20�{5 �@�@��15�|2�~2��5��15�|4��5 �T ���̌������,
�U �S6����2��,6�~5��2��15�ʂ� �@��2�����2��,1�ʂ� 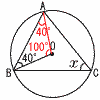 �@��4���甒2��,4�~3��2��6�ʂ� �@��4���甒2��,4�~3��2��6�ʂ�
�V (�E�}�Q��) ��OAB�͓ӎO�p�` �@��AOB��180�|40�~2��100�� �@��x��100��2��50��
�@�@�@�Z �@�A�@�Z �@�B�@�~ �@�C�@�~ �@ |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 12��t�� | �P (1) 15�|21���|6 �@(2) 3a�{5b�{4a��7a�{5b �@(3) (x2�{2xy�{y2)�|(x2�|2xy�{y2)��4xy �Q (1) (x�|1)(x�{1)�|2x��62 �@�@�@x2�|1�|2x�|62��0���,x2�|2x�|63��0��, �E �@(2) (x�|9)(x�{7)��0 �@�@�@�@x��0������, x��9 �R (1) �G�@��4��2(�L����) �@ (2) 90n��32�~(2�~5)n���������ɂȂ�悢����, �@�@�@�@n��2�~5��10 �S (1) Q3�\Q1��14�|8��6(�_) �@(2) Q3(24�E25�l��)��14�_������, �@�@�@�@25�l��(5�l)��16�_ �@�@25�`32�l�ڂ�8�l���,8�|5��3(�l) �T (1) ��AB����4�{ �Ίp��,AH����4�{ �@�@�@�m����(4�{4)��(8�~7��2)��8��28��2/7 �@ (2) �Ίp��AC��,AF��,AG�����e4�{���� �@�@�@�m����(4�~3)��(8�~7��2)��12��28��3/7 �U (1) 3x�{2y��7�c�A �� 5x�|4y��19�c�C�� �@�@�@�@�@�A�������ĉ�����, ��_��(3,�|1) �@ (2) 2x�{ay��11��(3,�|1)���������, 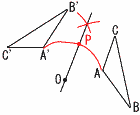 �@�@�@�@6�|a��11��, a���|5 �@�@�@�@6�|a��11��, a���|5�V (1) �C(��]�ړ�������~) �@(2) �E�} �@�EO�𒆐S��,���aOA�� �@�@�@��AA'������ �@�E����AA'�̐�������l �� �@�@�@���� �@�E��AA'��l �̌�_��P |
16�x�R�� | �P 9�|7��2 �Q �|25�~2���|50 �R ��120����15����8��2��2 �S 3a�{4�|2a�{4��a�{8 �T �㎮�~6�{�������,7x��42��,x��6 �@����������ɑ������,30�|3y��18��,y��4 �@�����, x��6, y��4 �U ���̌������,
 �W �S�̂̐����`�|�����̐����` �W �S�̂̐����`�|�����̐����`�@�@��n2�|(n�|2)2��4n�|4 (��) [�ʉ�] �@�c���~2�{(�����|2)�~2 �@�@��2n�{2(n�|2)��4n�|4 (��) 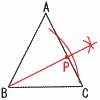 �X (�E�\�Q��) �X (�E�\�Q��)
�@��ABP��, �@�@��APB��180�|(54�{36)��90�� �@B����AC�ɐ��������낹�悢 |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| �m�g�b�v�ɖ߂��n�@�m�O�y�[�W�ɖ߂��n�@�m���y�|�W�ɐi���n |