全国公立高校入試 　１番問題　【令和７年春】

（３１）鳥取県

学習日　　　 月　　 　日（　　　）

印刷して、紙の上でやってネ！ 　印刷用

１	(1)	5－7	５	二次方程式 x2－3x－1＝0 を解きなさい。
	(2)	3√2＋ 　4 √2
	(3)	x＋2y － x－y 　2 3	６	次のア～工のうち,yがxの一次関数であるものを2つ選び,記号で答えなさい。 　ア　気温x℃のときの降水量ymm 　イ　分速xmで７分間進むときの道のりym 　ウ　１辺の長さがxcmの正方形の面積ycm2 　エ　300mL のジュースを,xｍL飲んだときの残りyｍL
	(4)	－ a3b÷(－ ab
２	次の数量を表す式を書きなさい。ただし,消費税は考えないものとする。 　a円のノートを, 3割引で買ったときの代金		７	2つの関数y＝ax2とy＝3x＋2について,xの値が１から３まで増加するときの,それぞれの変化の割合が等しくなるような,aの値を求めなさい。
３	2x2－18 を因数分解しなさい。
４	連立方程式 x＋y＝2 を解きなさい。 3x＋4y＝3		８	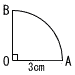右の図のおうぎ形OABについて,直線OBを回転の軸として1回転させてでき立体の体積を求めなさい。 　(次頁につづく)

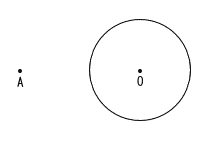
９	下の図において,円Oと,円Oの外部に点Aがある。次の条件を満たす点Pを作図しなさい 　ただし,作図に用いた線は明確にして,消さずに残しておき,作図した点Pには記号Pを書き入れなさい。 　条件 ① 点Pは円Oの円周上の点であり,直線AOより上側にある。 ② ∠APO＝90°である。	10	【操作①】：点Qは２回目に出た目の数だけ反時計回りに正五角形の頂点を１つずつ移動する。 【操作②】：点Qは２回目に出た目の数だけ時計回りに正五角形の頂点を１つずつ移動する。 　 　例　　【操作①】のとき　　　【操作②】のとき 　　　　　 　次の解答は,点Pと点Qが移動したとき,正五角形の同じ頂点にある確率を【操作①】の場合と【操作②】の場合について,それぞれ求めたものである。 　ただし,さいころは6つのどの目が出ることも同様に確からしいものとする。 　解　答 　さいころを２回投げたときの目の出方は［ア　］通り。 【操作①】のとき 　点Pと点Qが正五角形の同じ頂点にあるときは,さいころの出た目の差が0か5となればよいので,求める確率は［イ　］である。 【操作②】のとき 　点Pと点Qが正五角形の同じ頂点にあるときは,さいころの出た目の［ウ　］となればよいので,求める確率は［エ　］である。 (1) 解答の［ア　］, ［イ　］にあてはまる数を,それぞれ求めなさい。 (2) 解答の下線部を参考にして,さいころの目の出方について［ウ　］に適切な語句を入れなさい。また,［エ　］にあてはまる数を求めなさい。
10	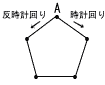右の図のように正五角形があり,1つの頂点をAとする。はじめに点Pと点Qは頂点Ａの位置にある。１から６までの目がある１つのさいころを２回投げて,点Pは１回目に出た目の数だけ反時計回りに正五角形の頂点を１つずつ移動する。また,点Qは２回目に出た目の数だけ次の【操作①】または【操作②】にしたがって移動する。 　例えば,１回目に出た目の数が3,2回目に出た目の数が6であるとき,点Pと点Qの位置は,あとの例のようになる。