Ｒ７年千葉県

あ～せには,あてはまるものをそれぞれ答えなさい。　

１

(1)

15十(－7)×3

５

　下の図のように,AD＝1cm,AE＝√3cm,EF＝2cmの直方体と,A,B,C,D,E,F,G,Hの文字が1つずつ書かれた8枚のカードがある。この8枚のカードをよくきって,同時に2枚のカ－ドをひく。ひいたカ－ドに書かれた文字と直方体の頂点の文字は対応しているものとし,ひいたカードに書かれた2つの文字の頂点を結んでできる線分について考え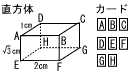

る。例えば,AとBの文字が書かれたカードを同時にひいた場合は,線分ABについて考える。
　ただし,どのカードをひくことも同様に確からしいものとする。

(2)

　(6a＋10b)÷2十4a

(3)

　(x＋y)²－(x－y)²
　

２

　連続する3つの正の整数がある。最も小さい数と最も大きい数の積から,中央の数の2倍の数をひくと62になる。
　中央の数をxとするとき,

(1)

　xについての方程式として最も適当なものを1つ選び,符号で答えなさい。
　ア　x²－64＝0　　　　イ　x²－4x－60＝0
　ウ　x²－2x－63＝0　　工　x²＋16x＋64=O

(1)

　ひいた2枚のカードに書かれた2つの文字の頂点を結んでできる線分の長さが2cmである確率は[か] / [き]である。
　

(2)

　中央の数xは[ あ　]である。

　

(2)

ひいた2枚のカードに書かれた2つの文字の頂点を結んでできる線分の長さが2cmより長い確率は[く] / [け]である。
　

３

(1)

　正しくないものを1つ選び,符号で答えなさい。
　ア 5の平方根は√5と－√5である。
　イ √2は循環しない無限小数である。
　ウ正の数a,bについて,a＜bならば√a＜√bである。
　工 √4は無埋数である。

６

　3つの直線 3x＋2y＝7, 5x－4y＝19, 2x＋ay＝11 が1点で交わるとき,

(1)

　3つの直線の交点の座標は( こ,さし )である。
　

(2)

　√90nの値が自然数となるような最も小さい自然数nは[ いう　]である。
　

(2)

　aの値は[すせ]である。
　

４

　生徒32人に,1問4点,全部で5問の漢字テストを行った結果,次の□のとおりになった。ただし,1問に対する得点は,0点または4点だけとする。

　・第1四分位数は8点　・第2四分位数は12点
　・第3四分位数は14点　・得点が16点の生徒は5人

７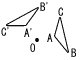

　図のように,△ABCがある。この△ABCを,点Oを回転の中心として反時計回りに110°だけ回転移動させたものが△A'B'C'である。

　

(1)

　32人の得点の四分位範囲は[ え　]点である。

　

(1)

　図の説明として正しくないものを,次のア～エのうちから1つ選び,符弓で答えなさい。
　ア　OA＝OA'である。
　イ　点Aが点A'まで移動した跡は,直線である。
　ウ　∠COC'＝1l0°である。
　エ　∠AOA'＝∠BOB'である。

(2)

32人のうち,得点が20点の生徒は[ お　]人である。

　　

(2)

　Aを,点Oを回転の中心として反時計回りに55°だけ回転移動させた点Pを作図しなさい。また,点Pの位置を示す文字Pも書きなさい。
　ただし,三角定規の角を利用して直線をひくことはしないものとし,作図に用いた線は消さずに残しておくこと。