| 1 |
 5-(-4) 5-(-4)
|
7 |
下の図のような,線分ABを直径とする半円があり,線分ABの中点をOとします。点0を通って線分ABに垂直な直線と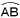 との との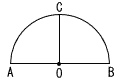 交点をCとします。 交点をCとします。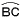 上にあって,∠POB=45°となる点Pを作図によって求めるとき,その作図の方法を説明したものとして,誤っているものを,あとのア~工から1つ選び,記号で答えなさい。 上にあって,∠POB=45°となる点Pを作図によって求めるとき,その作図の方法を説明したものとして,誤っているものを,あとのア~工から1つ選び,記号で答えなさい。
| ア |
∠COBの二等分線と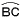 との交点をPとする. との交点をPとする. |
イ
|
点Aと点Cを結び,∠CABのn二等分線と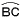 との交点をPとする. との交点をPとする. |
ウ
|
点Bと点Cを結び,線分BCの垂直二等分線と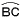 との交点をPとする. との交点をPとする. |
| エ |
線分OCの垂直二等分線と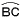 との交点をPとする。 との交点をPとする。 |
|
| 2 |
 |
|
6 |
÷(- |
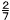 |
) |
|
| 3 |
 (-2a)2×5b (-2a)2×5b
|
| 4 |
等式 a+7b-3=0 をbについて解きなさい。
|
8 |
ある学年で,クロールで25mを泳いだときの記録をとりました。下の表は,このときの,A組の生徒25人とB組の生徒30人の記録を,累積度数をふくめて度数分布表に整理したものです。
A組とB組を比べたとき,180秒以上200秒未満の階級の累積相対度数が大きい組と,その累積相対度数を答えなさい。
| 階級(秒) |
A 組 |
B 組 |
| 度数(人) |
累積度数(人) |
度数(人) |
累積度数(人) |
以上 未満
140~160 |
4 |
4 |
3 |
3 |
| 160~180 |
5 |
9 |
6 |
9 |
| 180~200 |
7 |
16 |
9 |
18 |
| 200~220 |
6 |
22 |
10 |
28 |
| 220~240 |
3 |
25 |
2 |
30 |
| 合計 |
25 |
- |
30 |
- |
|
| 5 |
|
| 6 |
yはxの2乗に比例し,x=6のときy=-9です。このとき,yをxの式で表しなさい。
|
 交点をCとします。
交点をCとします。