|
(31)鳥取県 | 学習日 月 日( ) |
| 1 | (1) | 6 | 3枚の硬貨を同時に投げるとき,少なくとも1枚は表となる確率を求めなさい。 ただし,硬貨を投げるときの表,裏の出かたは,同様に確からしいものとする。 |
||||||
| (2) |
|
||||||||
| (3) | 3√3-√12 |
7 |
|
||||||
| (4) | 3(2x-1)-(x-2) |
次の図のように2本の棒で1個の部品を作り,この部品を横に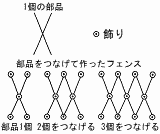 つなげてフェンスを作る。そして,棒の交わる部分と先端には飾りをつける。部品2個をつなけてフェンスを作った場合は飾りが8個,部品3個の場合は飾りが11個必要になる。ともこさんとたけおさんは,部品n個をつなげてフェンスを作ったとき,飾りが何個必要になるかを考えた。 つなげてフェンスを作る。そして,棒の交わる部分と先端には飾りをつける。部品2個をつなけてフェンスを作った場合は飾りが8個,部品3個の場合は飾りが11個必要になる。ともこさんとたけおさんは,部品n個をつなげてフェンスを作ったとき,飾りが何個必要になるかを考えた。(1) ともこさんは,必要な飾りの個数について,次のように考えた。
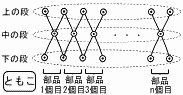 (次頁につづく) |
|||||||
| (5) | -3xy×2x3y2÷(-x2y) |
||||||||
| 2 | 8 | ||||||||
| 3 | 二次方程式 5x2-x-1=0 を解きなさい。 |
||||||||
| 4 |
|
||||||||
| 5 | 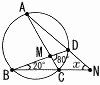 右の図において,∠xの大きさを求めなさい。 右の図において,∠xの大きさを求めなさい。ただし,4点A,B,C,Dは円周上の点であり,点Mは直線ACと直線BDの交点,点Nは直線ADと直線BCの交点である.。 |
||||||||
| 8 | (2) たけおさんは,必要な飾りの個数について,次のように考えた。
次のたけおさんのノートを参考にして,この式の[ ア ] [ イ ]にあてはまる文字式をそれぞれ求めなさい。 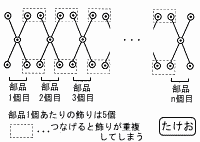 |
10 | 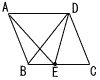 右の図のように平行四辺形ABCDにおいて,辺BC上にDC=DEとなる点Eをとる。このとき,△DBC≡△EADであることを次のように証明した。 右の図のように平行四辺形ABCDにおいて,辺BC上にDC=DEとなる点Eをとる。このとき,△DBC≡△EADであることを次のように証明した。証明の[ ア ]には適切な式を,[ イ ]には③が成り立つ適切な理由を書き,証明を完成させなさい。 (証明) △DBCと△EADで, 仮定より, DC=ED …① 平行四辺形の2組の向かい合う辺は, それぞれ等しいので, [ ア ] …②
したがって, ∠DCB=∠EDA …③ ①,②,③より,2組の辺とその間の角が, それぞれ等しいので, △DBC≡△EAD (証明終) |
||
| 9 | 図において,△ABCの辺AB,ACの長さはそれぞれacm,bcmである。このとき,辺BC上に,BP:PC=a:bとなる点Pを作図しなさい。 ただし,作図に用いた線は明確にして,消さずに残しておき,作図した点Pには記号Pを書き入れなさい。 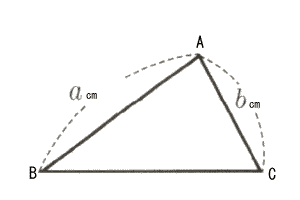 |
| [トップに戻る] [前ページに戻る] [次ペ-ジに進む] [答のペ-ジに進む] |