|
正 答 4 | |||
| 25 滋賀県 〜 32 島根県 |
|
正 答 4 | |||
| 25 滋賀県 〜 32 島根県 |
| 25滋賀県 | 1 −12+7=−5
これを下式に代入して,20+2y=6で,y=−7 よって, x=4,y=−7 5 2√2(4−√2)=8√2−4 6 与式=x2+2x+1−x2+2x=4x+1 =4× 7 8 基準点をxとすると, (7−13+5−9+20)÷5+x=67 9 右図 ・最小値=76−48=28 ・第1四分位数=62−20=42 |
28兵庫県 | 1 −3 2 6x+3y−x+4y=5x+7y 3 3√5−2√5=5√5 4 解の公式より,
3=a/(−6)で,a=−18
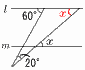 7
7 8 (右図参照) ∠x=60−20=40° |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 26京都府 | 【 前期 】 1 −27+18=−9
11<√125<12で,整数部分は 11 7 2で割って,x2−9x+6=0 解の公式より,
9 累積が増えていないから, X=0 Y=25−(1+0+2+…+1)=25−18=7 Z=0.96−0.60=0.88 【 中期 】 1 6+50=56 2 4x+2y−2x+
4 与式=(x−y−5)2=(7+6−5)2=64 5 2x(4x−11)=0より, x=0, 6 y=ax2に(3,−54)を代入すると, 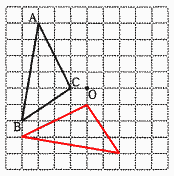 −54=32aで,a=−6 −54=32aで,a=−6よって, y=−6x2 7 右図 8 異色の確率 =1−同色の確率 2個の取り出し方は 5×4÷2=10通り 同色は,(赤赤) (白白) の2通り よって,異色の確率=1−2/10= |
29奈良県 | 1 (1) −3+7=4 (2) 6x−3+x−4=7x−7
2 解の公式より,
4 y= 4=a/(−6)で,a=−124
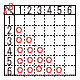 x=−24/3=−8 x=−24/3=−85 (右図参照) 確率=15/36= 6 (右下図参照) 立体=円錐(底面半径4,高さ3)×2 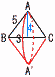 =( =(7 下図  8 (1) イ,ウ (2) 生徒を無作為に抽出していないから |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 30和歌山県 |
(4) 2√7−√7+3√7=4√7 (5) a2+10a+25−a2+10a−16=20a+9 2 x+2=±√13より, x=−2±√13 3 √126n=3√14nより, n=14 4 y=
(2) ア 180 イ GJ (GD,JDも可)  6 (右図参照) △OADで, 6 (右図参照) △OADで,∠O=2∠C=2∠x(中心角) ∠A=∠C=∠x(錯角) 2∠x+∠x=180−114=66° 3∠x=66より, ∠x=22° |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 27大阪府 | 【 A 】 1 6+2=8
4 x−3+4x+4=5x+1 5 6x2y 6 6√2−2√2=4√2 2番問題の一部 〜おまけ〜 1 3×6−5=18−5=13 2 −4,−3,…,1,2の 7個 3 イ 4 上式−下式より,4x=−4で,x=−1 これを下式に代入して,−1+2y=15 2y=16で,y=8 よって, x=−1,y=8 【 B 】 1 1−6=−5 2 3x−27y+4x+28y=7x+y
5 7+4√14+8=15+4√14 2番問題の一部 〜おまけ〜 1 8×(−3)+42=−24+16=−8 2 ウ(正+正=正となるから)
3 解の公式より,
5 (右表参照) 取り出し方は全部で, 5×4÷2=10通り 表より,b−aが偶数は3通り よって,確率= <別解>2数をx,yとすると, b−a=xy−(x+y)=(x−1)(y−1)−1 ←偶数 (x−1)(y−1)が奇数,すなわちxもyも偶数で あればよいから,3通り |
31鳥取県 |
3 解の公式より, 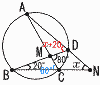
5 (右上図参照) ∠ADB=x+20(△DBNの外角)…ア ∠ACB=80−20=60°(△MBCの外角)…イ ア=イより,x+20=60で, ∠x=40° 6 1枚は表の確率=1−(3枚とも裏の確率) =1−( 7 2乗の比較から, √31, 8/√2, 6 8 (1) 上の段の飾りと下の段の飾りの総数 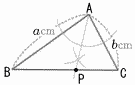 (2) ア 5n イ n−1 (2) ア 5n イ n−19 右図 ・∠Aの2等分線を引く ・BCとの交点をPとする 10 (右下図参照) ア BC=AD 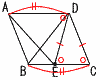 イ イ仮定より,△DCEはDC=DEの 二等辺三角形 二等辺三角影の2つの底角は 等しいので,∠DCB=∠DEC 平行線の錯角は等Lいので AD‖BCから,∠DEC=∠EDA |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 32島根県 | 1 5−12=−7 2 12−7=5 3 5(x−3)=3xより, x=15/2 4 上式+下式×3より,5x=10で,x=2 これを下式に代入して,2−y=3で,y=−1 よって, x=2,y=−1 5 x−2=±√7より, x=2±√7 6 (1) xy=20 (2) 30−5a>b 7 ア,イ,エ 8 ∠ADB=90°(直径に対する円周角)だから, ∠x=90−34=56° 9 (1) エ (2) ウ, オ |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| [トップに戻る] [前ページに戻る] [次ペ−ジに進む] |