|
(30)和歌山県 | 学習日 月 日( ) |
| 1 | (1) | 5 | 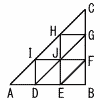 AB=BCの直角二等辺三角形ABCがある。右の図のように,辺ABを3等分する点をAに近いほうからD,E,辺BCを3等分する点をBに近いほうからF,G,辺CAを3等分する点をCに近いほうからH,I
とし,それぞれ点を結ぶ。また,線分EHと線分FI の交点をJとする。 AB=BCの直角二等辺三角形ABCがある。右の図のように,辺ABを3等分する点をAに近いほうからD,E,辺BCを3等分する点をBに近いほうからF,G,辺CAを3等分する点をCに近いほうからH,I
とし,それぞれ点を結ぶ。また,線分EHと線分FI の交点をJとする。(1) △ADIと合同な三角形のうち,平行移動だけで△ADI の位置に移るものは△ADI 以外にいくつあるか,求めなさい。 (2) △DEJ を△GHJ の位置に移す方法を次の2通り考えた。 次の[ア]にはあてはまる数を,[イ]にはあてはまる直線を答えなさい。
|
|||||||||
| (2) | 6+ |
|||||||||||
| (3) | -2(a-b)+5(2a-b) |
|||||||||||
| (4) | √28-√7+√63 |
|||||||||||
| (5) | (a+5)2-(a-8)(a-2) |
|||||||||||
| 2 | 次の二次方程式を解きなさい。 (x+2)2=13 |
|||||||||||
| 3 | √126nの値が自然数となるような自然数nのうち,最も小さいものを求めなさい。 |
6 | 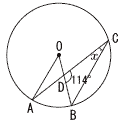 右の図のように,円Oの周上に3点A,B,Cがあり,線分OBと線分ACの交点をDとする。 右の図のように,円Oの周上に3点A,B,Cがあり,線分OBと線分ACの交点をDとする。OA∥CB,∠BDC=114°のとき,∠xの大きさを求めなさい。 |
|||||||||
| 4 | yはxに反比例し,x=2のとき,y=-3である。 このとき,yをxの式で表しなさい。 |
|||||||||||
| [トップに戻る] [前ページに戻る] [次ペ-ジに進む] [答のペ-ジに進む] |