|
(12)千葉県 | 学習日 月 日( ) |
| あ~ちには,あてはまるものをそれぞれ答えなさい。 | |||||||||||||
| 1 | (1) | 5 | 大小2つのさいころを同時に投げ,大きいさいころの出た目の数をa,小さいさいころの出た目の数をbとし,(a,b)を座標とする点Pをとる。 例えば,下の図の点Pは,大きいさいころの出た目の数が3,小さいさいころの出た目の数が4のときの座標(3,4)を表したものである。 ただし,原点Oから点(1,0)までの距離及び原点Oから点(0,1)までの距離をそれぞれ1cmとする。 また,さいころを投げるとき,1から6までのどの目が出ることも同様に確からしいものとする。 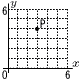 (1) 点Pが直線y=x上の点となる (1) 点Pが直線y=x上の点となる
|
||||||||||
| (2) | a2b÷3a×(-9a) | ||||||||||||
| (3) | (√7+√3)(√7-2√3) | ||||||||||||
| 2 | ある数xを2乗した数と,xを2倍した数との和は5である。 (1) xについての方程式として最も適当なものを,次のア~工のうちから1つ選び,符号で答えなさい。 ア x2+2x+5=0 イ x2-2x+5=0 ウ x2+2x-5=0 エ x2-2x-5=0 (2) ある数は あい±√う である。 |
||||||||||||
| 3 | (1) | 次のア~エのうち,標本調査を行うことが最も適しているものを1つ選ぴ,符号で答えなさい。 ア 国勢調査 イ 川の水質検査 ウ 学校で行う生徒の歯科検診 エ A中学校3年生の進路希望調査 |
6 | 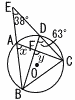 図のように,4点A,B,C,Dが円Oの円周上にあり,弦BAを延長した直線と弦CDを延長した直線の交点をE,線分ACと線分BDの交点をFとする。∠BEC=38°,∠BDC=63°であるとき, 図のように,4点A,B,C,Dが円Oの円周上にあり,弦BAを延長した直線と弦CDを延長した直線の交点をE,線分ACと線分BDの交点をFとする。∠BEC=38°,∠BDC=63°であるとき,(1) xで示した∠BACの大きさは すせ である。 (2) yで示した∠BFCの大きさは そた である。 |
|||||||||
| (2) | 袋の中に,同じ大きさの白い卓球の球だけがたくさん入っている。この白い球の個数を推定するために,色だけが違うオレンジ色の球30個をその袋に入れてよくかき混ぜ,そこから無作為に10個の球を抽出したところ,オレンジ色の球が3個含まれていた。 はじめに袋の中に入っていた白い球は,およそ えお個と推定できる。 |
||||||||||||
| 4 | (1) | 立方体の展開図として正しくないものを,次のア~工のうちから1つ選び,符号で答えなさい。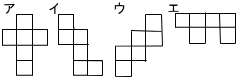 |
7 | 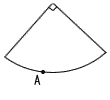 この円錐の展開図の底面の部分である円が点Aを通るとき, (1) 側面の部分であるおうぎ形の半径日面の部分である円の半径の ち 倍である。 (2) 底面の部分である円の中心0を作図によって求めなさい。また,中心0の位置を示す文字Oも書きなさい。 ただし,三角定規の角を利用して直線をひくことはしないものとし,作図に用いた線は消さずに残しておくこと。 |
|||||||||
| (2) | 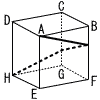 右の図のように,1辺が3cmの立方体がある。この立方体の表面に,頂点Aから頂点Hまで,辺BFと辺CGを通るようにひもをかける。ひもの長さが最も短くなるときのひもの長さは か√きく cmである。 右の図のように,1辺が3cmの立方体がある。この立方体の表面に,頂点Aから頂点Hまで,辺BFと辺CGを通るようにひもをかける。ひもの長さが最も短くなるときのひもの長さは か√きく cmである。 |
||||||||||||
| [トップに戻る] [前ページに戻る] [次ペ-ジに進む] [答のペ-ジに進む] |