|
���@���@�Q | |||
| �X�@�Ȗ،��@�`�@16�@�x�R�� |
|
���@���@�Q | |||
| �X�@�Ȗ،��@�`�@16�@�x�R�� |
| �X�Ȗ،� | �P 12 �Q 2��7�{��7��3��7 �R �|2,�|1,0�C1,2, �� 5�� �S (x�{2)(x�{3)��0���, x���|2,�|3 �T y��
�W 85�`100�̊K����,7��20��0.35 �@�`�Q�Ԗ�� �i���܂��j �P 28.5��a��29.5
�@�����������,x��350,y��50 �����,���鋗����350m,����������50m |
13�����s | �P �|36��9�|4���|4�|4���|8
�S 2x�{x��4�{8 �@�@3x��12���, x��4 �T �㎮�~3�|�����~5���,y���|3 �@����������ɑ������, �@�@3x�|12��6��,x��6 �@�����, x��6,y���|3 �U x�|8���}1���,x���}1�{8 �@x��9,7 �V �G �@�A A�g�͂��Ȃ�(��) �@�C �ő��B�g(��) �@�E ���Ȃ��Ƃ͌���Ȃ�(��) �@�G B�g��23�|14��9m��,�ŏ�(��) �W 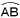 �� ��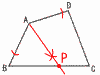 �@x��90�~ �@x��90�~�X �E�} �E��BAD�̓��������� �E��BC�Ƃ̌�_��P�Ƃ��� |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 10�Q�n�� | �P (1) 7�|2��5 �@(2) 3x�{7�|x�{1��2x�{8  �@(3) 3a�|2 �@(3) 3a�|2�Q (x�|8)(x�{3) �R �C �G �S (�E�}�Q��) �@��ʂ̉~���������`�̉���10�� �@52���~2�{6�~10����110��cm2 �T ���̌������,
�U 180�|64�~2��52�� �V ��412�|402����1681�|1600����81��9cm
�@11/36 �X y��ax2�Ƃ����, (10,10)��������, �@102a��10���,a�� y�� �@y�� �@ |
14�_�ސ쌧 | �A �|6�i��2�j
�I (x2�|4x�{4)�|(x2�|5x�|24) �@�@��x�{28�i��4�j �@�`�Q�Ԗ�� �i���܂��j �A ����������,
�C ���̌������,
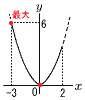 �E (�E�}�Q��) �E (�E�}�Q��)x���|3�̂Ƃ�,�ő�ly��6 �@y��ax2��(�|3,6)��������, �@�@6��(�|3)2a���,
�I �̐ρ� �J 3y��3�~47��141 �@x2�|9y2��(x�{3y)(x�|3y) �@�@��(143�{141)(143�|141)��284�~2 �@�@��568�i��3�j |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 11��ʌ� | �P 2x�@�@�Q �|8�|1���|9
�@�|x��4��, x���|4 �T 2��3�{��3��3��3 �U (x�|9)(x�{8) �V �㎮�~3�{�������, �@22x��22��,x��1 �@������㎮�ɑ������, �@�@6�|y��10��,y���|4 �����, x��1,y���|4 �W ���̌������,
10 10�����̌ʂɑ���~���p�� �@10�����̒��S�p�̔�����,18�� ��EAH��18�~3��54��,��AHB��18�� ��AKH��,x��180�|54�|18��108��  11(�E�}�Q��) 3�{ 11(�E�}�Q��) 3�{12 �G �A�c�����l��12�`16�� �C�c4��20��0.20 �E�c12�`16��,14�� 13 10x�{y��11,12,�c,66  ���̂���,7�̔{���� ���̂���,7�̔{�����@14,21,35,42,56,63��6�ʂ� �����,�m����6/36�� 14 (�E��}�Q��) �̐ρ�(62��-22��)�~6��192��cm3 15 (�E���}�Q��) �����̕����̖ʐς��@�ƍl���� �@�d�Ȃ遁�@�~(x�|1)��x�|1 �@�d�Ȃ�Ȃ����B�~2�{�A�~(x�|2)��2x�{2 (x�|1)�F(2x�{2)��2:5���,5x�|5��4x�{4 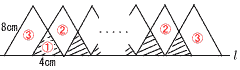 �����,x��9 �����,x��916 (��) �@���ԇ@�����ԇA�̕���,��1�l���ʐ�����3�l���ʐ�������ɋ߂��B |
15�V���� | �P �|2 �Q 6a�|3b�{5a�|10b��11a�|13b �R 2x �S 3����2�悷���,
�T x�{5���}��13���, x���|5�}��13 �U y�� �@3��a/500��,a��1500
�@�����,��x��72��2��36�� �W ���ʂ�x�Ƃ����,
�@x�{300��3000���,x��2700�� �@ |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 12��t�� | �P (1) �|4�{6��2
�@�@�@��7�|��21�|2�E3��1�|��21 �Q (1) x2�{2x��5���, �E �@ (2) ���̌������,
�@ (2) �F�̔䗦���琄��
 �S (1) �G �S (1) �G�@ (2) (�E�}�Q��) �@�@�@AB����32�{92����90 �@�@�@�@��3��10cm �T (1) (1,1) (2,2) �c (6,6) ��6�ʂ��, �@�@�@�@�m����6/36�� �@ (2) OP����x2�{y2��4 �@�@2�悵��,x2�{y2��16���, �@�@�@(1,1) (1,2) (1,3) (2,1) (2,2) (2,3) �@�@�@ (3,1) (3,2) ��8�ʂ��, �@�@�m����8/36�� �U (1) ��BAC����BDC��63�����, x��63 �@ (2) ��EBD��,��EBD��63�|38=25�� �@�@�@��BFC��63�{25��88�����,y��88 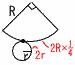 �V (1) (�E�}�Q��) �V (1) (�E�}�Q��)�@��`�̌ʁ�2R�~ �@�~����2r �c�C �@�@�A���C���,  (2) �E�} (2) �E�}�E����BA������ �EAB��2�����_C����} �EAC��2�����_D����} �E���SA,���aAD�̉~����} ��~�ƒ����̂���1�̌�_��O�Ƃ��� |
16�x�R�� | �P 7�|8���|1
�R 2��6�|��6����6 �S 8a�{4b�|5a�{b��3a�{5b �T �����~3�|�㎮�~4���,7x���|7��,x���|1 �@������㎮�ɑ������,�|2�{3y��4��,y��2 �@�����, x���|1,y��2 �U �̐ρ�32���~10��90��cm3
�W 4a�{3b��7000 �X �ς������̊m����1�|(�ς���̊m��)
 10 �E�} 10 �E�}�E��A�̓��������� �EBC�̌�_��P |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| �m�g�b�v�ɖ߂��n�@�m�O�y�[�W�ɖ߂��n�@�m���y�|�W�ɐi���n |