| 13 |
 1から6までの目が出る大小2つのさいころを1回投げて,大きいさいころの出た目の数をx,小さいさいころの出た目の数をyとします。このとき,10x+yが7の倍数になる確率を求めなさい。 1から6までの目が出る大小2つのさいころを1回投げて,大きいさいころの出た目の数をx,小さいさいころの出た目の数をyとします。このとき,10x+yが7の倍数になる確率を求めなさい。
ただし,大小2つのさいころは,どの目が出ることも同様に確からしいものとします。
|
16 |
次は,先生とSさん,Tさんの会話です。これを読んで,下の問に答えなさい。
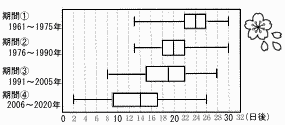
先生「わたしたちの中学校では,校庭にある桜の開花日を生徒会の役員が毎年記録しています。次の図は,1961年から2020年までの記録を,3月15日を基準日としてその何日後に開花したかを,期間①から期間④の15年ごとの期間に分け,箱ひげ図にそれぞれ表したものです。これを見て,気づいたことを話し合ってみましょう。」
Sさん
|
「4つの箱ひげ図を見ると,桜の開花日は60年間でだんだん早くなっているようだね。」 |
Tさん
|
「だけど期間①と期間②の箱ひげ図は,最も早い開花日と最も遅い開花日が同じ位置だよ。それでも,,開花日は早くなっているといえるのかな。」 |
Sさん
|
「期間①と期間②の箱ひげ図を
比べると,
から,期間①より期間②の方が,開花日は早くなっているといえると思うよ。」 |
問 会話中の□にあてはまる,開花日が早くなっていると考えられる理由を,第1四分位数,第3四分位数という二つの語を使って説明しなさい。
|
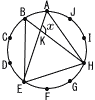 右の図のように,円周の長きを10等分する点A~J があります。△AEHと△BEHをつくり,辺AEと辺BHとの交点をKとするとき,∠AKHの大きさxを求めなさい。
右の図のように,円周の長きを10等分する点A~J があります。△AEHと△BEHをつくり,辺AEと辺BHとの交点をKとするとき,∠AKHの大きさxを求めなさい。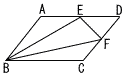 右の図のような平行四辺形ABCDがあり,辺AD,CDの中点をそれぞれE,Fとします。このとき,△EBFの面積は△DEFの面積の何倍になるか求めなさい。
右の図のような平行四辺形ABCDがあり,辺AD,CDの中点をそれぞれE,Fとします。このとき,△EBFの面積は△DEFの面積の何倍になるか求めなさい。 1から6までの目が出る大小2つのさいころを1回投げて,大きいさいころの出た目の数をx,小さいさいころの出た目の数をyとします。このとき,10x+yが7の倍数になる確率を求めなさい。
1から6までの目が出る大小2つのさいころを1回投げて,大きいさいころの出た目の数をx,小さいさいころの出た目の数をyとします。このとき,10x+yが7の倍数になる確率を求めなさい。
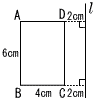 右の図のような,AB=6cm.,BC=4cmの長方形ABCDと直線l があり,辺DCと直線l の距離は2cmです。このとき,長方形ABCDを,直線l を軸として1回転させてできる立体の体積を求めなさい。
右の図のような,AB=6cm.,BC=4cmの長方形ABCDと直線l があり,辺DCと直線l の距離は2cmです。このとき,長方形ABCDを,直線l を軸として1回転させてできる立体の体積を求めなさい。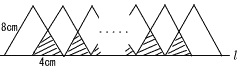 い部分の面積の比が2:5になりました。このとき,xの値を求めなさい。
い部分の面積の比が2:5になりました。このとき,xの値を求めなさい。