| 次の(1)~(15)の中から,指示された8問について答えなさい。 |
| 1 |
 6-2×5 6-2×5 |
11 |
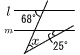 右の図で,2直線l,mは平行である。このとき,∠xの大きさを求めなさい。 右の図で,2直線l,mは平行である。このとき,∠xの大きさを求めなさい。
|
| 2 |
 5(x+2y)-2(4x-y) 5(x+2y)-2(4x-y) |
| 3 |
 90を素因数分解しなさい。 90を素因数分解しなさい。
|
12 |
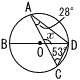 右の図で,4点A,B,C,Dは円Oの周上の点であり,線分BDは円Oの直径である。∠CAD=28°,∠ACD=53°のとき,∠xの大きさを求めなさい。 右の図で,4点A,B,C,Dは円Oの周上の点であり,線分BDは円Oの直径である。∠CAD=28°,∠ACD=53°のとき,∠xの大きさを求めなさい。
|
| 4 |
x=3,y=-2のとき,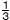 x2y3÷2xyの値を求めなさい。 x2y3÷2xyの値を求めなさい。
|
| 5 |
√32-√50+√27
|
13 |
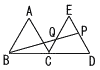 右の図のように,△ABCと△ECDは合同な正三角形であり,点B,C,Dは一直線上にある。点Pは辺DE上の点であり,点Qは線分BPと辺CEの交点である。AB=7cm,EP=3cmのとき,線分CQの長さを求めなさい。 右の図のように,△ABCと△ECDは合同な正三角形であり,点B,C,Dは一直線上にある。点Pは辺DE上の点であり,点Qは線分BPと辺CEの交点である。AB=7cm,EP=3cmのとき,線分CQの長さを求めなさい。
|
| 6 |
方程式 0.8x+4=1.5x-0.9 を解きなさい。
|
| 7 |
| 連立方程式 |
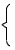 |
2x-y=7 |
を解きなさい。 |
| 5x+3y=1 |
|
14 |
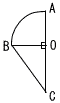  右の図のように,おうぎ形AOBと直角三角形BOCが同じ平面上にあり,OB=6cm,BC=10cm,∠AOB=90°,∠BOC=90°である。おうぎ形AOBと直角三角形BOCを合わせた図形を,直線ACを軸として1回転させてできる立体の体積を求めなさい。ただし,円周率をπとする。 右の図のように,おうぎ形AOBと直角三角形BOCが同じ平面上にあり,OB=6cm,BC=10cm,∠AOB=90°,∠BOC=90°である。おうぎ形AOBと直角三角形BOCを合わせた図形を,直線ACを軸として1回転させてできる立体の体積を求めなさい。ただし,円周率をπとする。
|
| 8 |
方程式 x2-2x=24 を解きなさい。
|
| 9 |
9 13 16 5 17
20 9 15 14 (点) |
右の表は,クイズ大会に参加した9人の得点である。表をもとにして,箱ひげ図をかくと,右の図のようになった。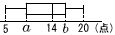 a,bの値を求めなさい。 a,bの値を求めなさい。
|
15 |
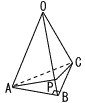  右の図のように,三角錐OABCがある。△ABCは直角二等辺三角形で,AB=BC=6cm,∠ABC=90°である。また,OA=OB=OC=9cmである。点Aから辺OBを通り,点Cまで最も短くなるようにひいた線と辺OBの交点をPとする。このとき,三角錐PABCの体積を求めなさい。 右の図のように,三角錐OABCがある。△ABCは直角二等辺三角形で,AB=BC=6cm,∠ABC=90°である。また,OA=OB=OC=9cmである。点Aから辺OBを通り,点Cまで最も短くなるようにひいた線と辺OBの交点をPとする。このとき,三角錐PABCの体積を求めなさい。
|
| 10 |
 n2-20n+91の値が素数となる自然数nの値をすべて求めなさい。 n2-20n+91の値が素数となる自然数nの値をすべて求めなさい。
|
 右の図で,2直線l,mは平行である。このとき,∠xの大きさを求めなさい。
右の図で,2直線l,mは平行である。このとき,∠xの大きさを求めなさい。 右の図で,4点A,B,C,Dは円Oの周上の点であり,線分BDは円Oの直径である。∠CAD=28°,∠ACD=53°のとき,∠xの大きさを求めなさい。
右の図で,4点A,B,C,Dは円Oの周上の点であり,線分BDは円Oの直径である。∠CAD=28°,∠ACD=53°のとき,∠xの大きさを求めなさい。 右の図のように,△ABCと△ECDは合同な正三角形であり,点B,C,Dは一直線上にある。点Pは辺DE上の点であり,点Qは線分BPと辺CEの交点である。AB=7cm,EP=3cmのとき,線分CQの長さを求めなさい。
右の図のように,△ABCと△ECDは合同な正三角形であり,点B,C,Dは一直線上にある。点Pは辺DE上の点であり,点Qは線分BPと辺CEの交点である。AB=7cm,EP=3cmのとき,線分CQの長さを求めなさい。
