全国公立高校入試 　１番問題　【令和６年春】	正　答　１
	１　北海道　〜　８　茨城県

１北海道	１ (1) −6 　　(2) 7−6＝1 　　(3) 3√2−√2＝2√2 ２ 2×5×7 ３ 1:x＝30:yより, y＝30x ４ �@ ウ　(傾きaは負) 　 �A ア　(切片bは正) ５ �@ エ　(左右に広がり) 　 �A ア　(右にかたより) ６ 右図 BCの中点をPとすればよい	５山形県	１ (1) −9＋6＋2＝−1 　(2) 　−14＋9 × −9 ＝ (−5)×(−9) ＝ 9 ＝ 12 5 12×5 12 　(3) 　10xy2×(−4x)2 ＝−5xy 　8x2y 　(4) 3√3＋√3＝4√3 ２ 4x2−1＝−4xで,4x2＋4x−1＝0 解の公式より, 　x＝ −2±√22−4×(−1) ＝ −2±2√2 4 4 　　＝ −1±√2 2 ３ (右図参照) ∠BAC＝∠BDC＝55° ∠A＋∠C＝180°だから, 　∠ACB＝180−(55＋42＋36)＝47° 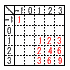４ (右表参照) 10÷25＝で, ウ ５ ア
２青森県	１ (1) 4＋1＝5　　(2) −24÷4＝−6 　(3) 　2(9x−6y) ＝−6x＋4y −3 　(4) 　5(2x＋y−1)−3(3x−2y＋3) 3×5 　　＝ x＋11y−14 15 　(5) √2(√3＋1)・√8(√3＋1)＝√16(√3＋1) 　　＝4√3＋4 ２ 3±4＝7,−1 ３ 印ありの比率＝ 24 ＝ 2 より, x 35 　x＝24×35÷2≒420　　およそ420個 ４ (x)2＋2×x×3＋32＝x2＋x＋9 ５ (右図参照) 最大値16より,a2＝16で,a＝4 最小値0より,b＝0 ６ (右下図参照)20°の回転 ∠x＝180−(125＋20)＝35° ７ x＝2,y＝2など ８ エ ・ア…y＝−2x＋3(正) ・イ…直線上のすべての点で 　　　成り立つ(正) ・ウ…x＝1のとき,y＝1(正) ・エ…傾き−2(誤)	６宮城県	１ −14 ２ 　 − ＝ ３ 3a−2b ４ 与式＝2a＋14b−8b＝2a＋6b 　　　＝2×(−5)＋6×＝−10＋1＝−9 ５ (x−3)(x−7) ６ y＝に(−2,9)を代入すると, 　　9＝a/(−2)で,a＝−18 　よって, y＝− 18 x ７ 3数を2乗すると, 10 7　9 だから, エ 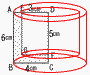８ (右図参照) 立体＝外円柱−内円柱 　＝42π×6−32π×5 　＝96π−45π＝51πcm3
３秋田県	１ 6−10＝−4 ２ 5x＋10y−8x＋2y＝−3x＋12y ３ 2×32×5 ４ 与式＝ 　x2y3 . ＝ xy2 ＝ 3×(−2)2 ＝2 3×2xy 6 6 ５ 4√2−5√2＋3√3＝−√2＋3√3 ６ 両辺×10より,8x＋40＝15x−9 　−7x＝−49で, x＝7 ７ 上式×3＋下式より,11x＝22 　x＝2で,これを上式に代入して, 　2×2−y＝7より,−y＝7−4＝3 　　よって, x＝2, y＝−3 ８ 移項して,x2−2x−24＝0 　(x−6)(x＋4)＝0より, x＝6,−4 ９ 9人の得点を小さい順に並べ替えて 　5 9 9 13 14 15 16 17 20 第1四分位数a＝9 第3四分位数b＝(16＋17)÷2＝16.5 10 与式＝(n−7)(n−13) ←どちらかが±1 n−7＝1のとき,n＝8（不適） n−7＝−1のとき,n＝6（適） n−13＝1のとき,n＝14（適） n−13＝−1のとき,n＝12（不適） 　よって, n＝6,14 11 (右上図参照) 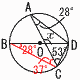∠x＝68−25＝43° 12 (右図参照) ∠B＝28°∠ACB＝37° 　∠x＝180−(28＋37)＝115° 13 (右図参照) 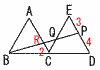PD＝4より,RC＝2で, 　△QRC∽△QPE(相似比2:3) CQ＝7×＝14/5cm 14 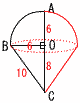(右下図参照) 回転体＝半球＋円錐 　＝π×63÷2＋π×62×8 　＝144π＋96π＝240πcm3 15 右下展開図アで, △ABP∽△OBM（相似比2:3)より, 　BP＝2cm…ウ 右下図イで,ACの中点をHとすると, 　△OHBで,OH＝√92−(3√2)2＝3√7 三角錐OABC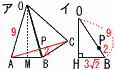＝(×62)×3√7 　　＝18√7…エ ウエより, 　三角錐PABC＝18√7× 　　　＝4√7cm3	７福島県	１ (1) 4 　(2) 　　2×15 . ＝− 　5×(−8) 　(3) 9x−2y 　(4) 3×3√2＝9√2 ２ (x＋y)2−1＝x2＋2xy＋y2−1 　〜２番問題 （おまけ）〜 １ 5a＋2b＝1020 ２ (5×4＋2)−(5×1＋2)＝22−7＝15 ３ △OBCは二等辺三角形だから, 　　∠BOC＝180−48×2＝84° 　∠x＝∠BOC＝84×＝42° ４ 76, 85, 88, 98, 102, 114, 118, 122, 143 　上位4つの中央値で, 　　Q3＝(118＋122)÷2＝120個 ５ 右図 ・直線OP上の点Pを通る垂線
		８茨城県	１ (1) −6 　(2) −3x−6y＋x−3y＝−2x−9y 　(3) 　3a2b×4b ＝2ab 　6ab 　(4) √12＋√18＝2√3＋3√2 ２ エ 　〜２番問題 （おまけ）〜 １ (右図参照) イ 　∠ACD＝74−39＝35° 　∠BCD＝60−35＝25° ２ ウ 　1 2 3 3 3｜4 5 6 7 9 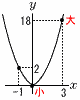　四分位数を求めて, 　　中央値Q2＝3.5　Q1＝3　Q3＝6 ３ ア ４ (右図参照) エ 　グラフは下に凸の放物線 　　x＝3のとき,最大値y＝18 　　x＝0のとき,最小値y＝0
４岩手県	１ 2　　２ 9x−6　　３ 8√6　　４ (x＋4)2 ５ 解の公式より, 　x＝ −(−3)±√(−3)2−4×1×(−5) ＝ 3±2√9＋20 2×1 2 　　＝ 3±√29 2 　〜２番問題 （おまけ）〜 ２ 10a＋b≧500 ３ y＝に,(2,2)を代入して, 　2＝ a より,a＝4 2 　y＝ 4 に,x＝8を代入して, y＝ 4 ＝ 　　 x 8	４岩手県	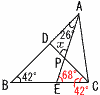４ (1) △ADE∽△ABCより, 　　　　　4:BC＝3:(3＋6) 　　　　　BC＝4×9÷3＝12cm 　(2) (右上図参照) △PECで, 　　∠E＝26＋42＝68°…ア 　　DB＝DCより,∠C＝42°…イ 　　アイより,∠x＝180−(68＋42)＝70° 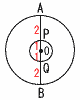　(3) (右図参照) 　AB＝6とすると 　　小円の半径OP＝1, 　　大円の半径OA＝3 　(小円の面積)：(大円の面積) 　　　＝12:32＝1:9で, 9倍