| １ |
(1) |
 －4－7
|
６ |
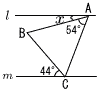 右の図のように,AB＝ACである二等辺三角形ABCがある。また,頂点Aを通る直線lと,頂点Cを通る直線m:があり,lとmは平行である。
このとき,∠xの大きさを求めなさい。
|
| (2) |
－2(x＋3y)＋(x－3y)
|
| (3) |
8xy2÷(－2x)
|
７ |
次の図は,ある都市における2003年,2012年,2021年の各月の最高気温をそれぞれ年別に箱ひげ図に表したものである。この箱ひげ図から読み取れることとして正しいものを,あとの①～⑤の中からすべて選び,番号を書きなさい。
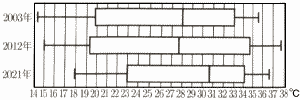
| ① |
第3四分位数は,2021年が最も大きい。 |
| ② |
四分位範囲は,2012年が最も大きい。 |
| ③ |
2021年では,最高気温が20で以下の月は１つしかない。 |
④
|
2012年では,25％以上の月が,最高気温が34℃以上である。 |
| ⑤ |
2003年では,最高気温の嘔均値は28℃である。 |
|
| (4) |
(√5＋1)2
|
| ２ |
x2－9y2 を因数分解しなさい。
|
| ３ |
二次方程式 2x2－x－2＝0 を解きなさい。
|
| ４ |
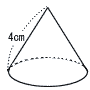 右の図のような母線の長さが4cmの円錐がある。この円錐の側面の展開図が半円になるとき,この円錐の底面の半径を求めなさい。
|
 |
| ５ |
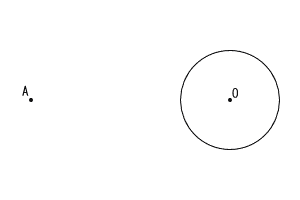
 右の図のような点Aと点Oを中心とする円Oがある。点Aから円Oにひいた2本の接線を作図しなさい。
ただし,作図には定規とコンパスを用い,作図に用いた線は消さずに残しておくこと。 |
印刷用