全国公立高校入試 　１番問題　【令和５年春】	正　答　６
	41　佐賀県　〜　47　沖縄県

　

41佐賀県	１ (1) −11 　(2) −2x−6y＋x−3y＝−x−9y 　(3) −4y2 　(4) 5＋2√5＋1＝6＋2√5 ２ (x＋3y)(x−3y) ３ 解の公式より, 　x＝ −(−1)±√(−1)2−4×2×(−2) 2×2 　　＝ 1±√1＋16 ＝ 1±√17 4 4 ４ 底面の円周＝側面(半円)の弧の長さ 　底面の半径をrとすると, 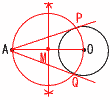　　2πr＝8π×で, r＝2cm ５ 右図 　AOを直径とする円を作図する ・AOの中点Mをかく ・AMを半径とする円Mをかく ・円Mと円Oの2交点P,Qをとる ・APとAQが2本の接線となる 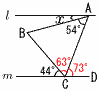６ (右図参照) 　∠ACB＝（180−54)÷2＝63° 　∠ACD＝180−(44＋63)＝73° 　∠x＋54＝73より, ∠x＝19° ７ �A,�C	44熊本県	１ 　2＋7 ＝ 9 　　２ 6−12＝−6 　7×2 14 ３ 8x＋9y＋7x−7y＝15x＋2y ４ 8a3b×9b ＝2a 36a2b2 ５ x2−4x−5＋x2＋4x＋4＝2x2−1 ６ √6＋3√6＝4√6 　〜２番問題の一部 （おまけ）〜 １ 2x＝−12で,x＝−6 ２ 解の公式より, 　x＝ −5±√52−4×2×(−1) 2×2 　　＝ −5±√25＋8 ＝ −5±√33 4 4 ３ y＝に(2,3)を代入して, 　3＝a/2で,a＝6 　y＝にx＝5を代入して, y＝ ４ △CABで,∠BAC＝(180−54)÷2=63° 　△CADで,∠CAD＝140÷2−54＝16° 　△OABで,∠OAB＝(180−140)÷2＝20° 　よって,∠OAD＝63−16−20＝27°
42長崎県	【　前期　】 １ 　1×3−1×2 ＝ 3−2 ＝ 　2×3 6 ２ 200×(1−0.3)＝200×0.7＝140円 ３ 5a＋10b＋2a−6b＝7a＋4b ４ 上式＋下式×2より, 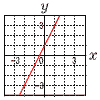　5x＝20で,x＝4 　これを上式に代入して, 　　4＋2y＝8で,y＝2 　よって, x＝4,y＝2 ５ 右上図 　y切片1,傾き2の直線 ６ （ア） (1+4+3+12+15)÷10 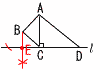　　　　＝35÷10＝3.5点 　(イ) 1÷10＝0.1 ７ (ア) 右図 ・Ｂからl に垂線をおろす 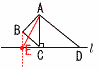(イ) (右下図参照) 　BE//ACだから, 　　△AEC＝△ABC 　両辺に△ACDを加えて, 　　△AED＝四角形ABCD ８ アプリB 　A…5000÷100＝50ポイントだが, 　　上限を超えるから,20ポイント 　B…5000÷200＝25ポイント 　　上限を超えないから,そのまま25ポイント 　　【　後期　】 １ 3＋18＝21 ２ 2x＋6y−x＋2y＝x＋8y ３ 　√2＋1 − 1×√2 ＝ √2＋1 − √2 　3 √2√2 3 2 　＝ 2√2＋2−3√2 ＝ 2−√2 3×2 6 ４ (x−1)(x＋6) ５ 解の公式より, 　x＝ −3±√32−4×2×(−4) 2×2 　　＝ −3±√9＋32 ＝ −3±√41 4 4 ６ x＝−1のとき,y＝−2×(−1)＋1＝3 　x＝2のとき,y＝−2×2＋1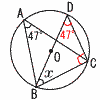＝−3 　よって, −3≦y≦3 ７ 17×17＝289 ８ (右図参照) 　△BCDで, 　　∠D＝∠A＝47° 　　∠C＝90° 　∠x＝180−(47＋90)＝43° 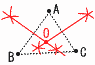９ 半径3cmの半球で, 　π×33×＝18πcm3 10 右図 ・2点を結ぶ線分の垂直二等分線 　を2本引き,その交点を中心Oとする	45宮崎県	１ 5 ２ −　　 ３ 5√2＋2√2−3√2＝4√2 ４ 移項して,3b＝a＋1 　3で割って,b＝ a＋1 　または,b＝ (a＋1) 3 ５ 上式を下式に代入して, 　　3x＋4(x−6)＝11 　　3x＋4x＝11＋24で,x＝5 　　これを上式に代入して, 　　　y＝5−6＝−1 　よって, x＝5, y＝−1 ６ 移項して,因数分解すると, 　　x(9x−5)＝0 　よって, x＝0, ７ エ 　ア…第3四分位数は30°より下 　イ…平均値は不明 　ウ…ひげの長さは日数に比例していない 　エ…範囲,四分位範囲ともに正しい 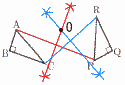８ 右図 ・APの垂直二等分線を引く ・CRの垂直二等分線を引く ･2直線の交点をOとする 　(BQの垂直二等分線でもよい)
		46鹿児島県	１ (1) 7−2＝5 　(2) 　5−2 × ＝ 3×1 ＝ 　10 10×3 　(3) x2＋2xy＋y2−x2−2xy＝y2 　(4) ±6,±5,…,±1,0 の13個 　(5) 3√2＝√18,2√3＝√12,4＝√16より, 　　　3√2＞4＞2√3だから, ア ２ 上式×2＋下式より, 　　　7x＝21で,x＝3 　　これを上式に代入して, 　　　9＋y＝8で,y＝−1 　よって, x＝3,y＝−1 ３ 20,60,110,150円の 4通り ４ ＝0.818181…だから, 1 ５ A中の度数＝20×0.35＝7人 　　B中の度数＝25×0.44＝11人 　よって, (7＋11)÷45＝0.40
43大分県	１ (1) 3 　(2) 6−9×2＝6−18＝−12 　(3) 　(x＋5y)＋4(x−y) 　8 　　＝ x＋5y＋4x−4y ＝ 5x＋y 8 8 　(4) 　4x2y ＋ xy3 ＝4x＋y2 xy xy 　(5) √12＋ 　3√3 ＝2√3＋√3 ＝3√3 √3√3 ２ (x−8)(x＋2)＝0より, x＝8,−2 ３ 5＜√6aが＜7 　各辺を2乗して,25＜6a＜49 　各辺を6で割って, 4.17＜a＜8.17 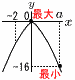　よって, a＝5,6,7,8 ４ (右図参照) 　最大値はx＝0のときで,b＝0 　最小値がx＝−2のときとすると 　　−(−2)2＝−4≠−16で不適 　最小値がx＝aのときとすると, 　　−a2＝−16で,a＝±4 　ところが,−2≦x≦aだから,a＝−4は不適 　よって, a＝4, b＝0 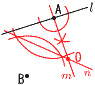５ 52π× 144 ＝25π× ＝10πcm2 360 ６ 右図 ・Aからl の垂線mを引く ・ABの垂直二等分線nを引く ・mとnの交点を中心Oとする	47沖縄県	１ −5＋7＝2　　　２ (−12)×＝−9 ３ 7＋10＝17 ４ 2√3＋3√3＝5√3 ５ 9a2×(−2b)＝−18a2b ６ 15x＋6y−12x＋4y＝3x＋10y 　〜２番問題の一部 （おまけ）〜 １ 移項して,5x−2x＝3＋6 　　　3x＝9で, x＝3 ２ 上式×2＋下式より, 　　　5x＝15で,x＝3 　　これを上式に代入して, 　　　2×3＋y＝5で,y＝−1 　よって, x＝3, y＝−1 ３ x2−32＝x2−9 ４ (x＋5)(x−3) ５ 解の公式より, 　x＝ −5±√52−4×2×1 2×2 　　＝ −5±√25−8 ＝ −5±√17 4 4 ６ (右図参照) 　2＜√5＜3, 3＜√11＜4より, 　　n＝3 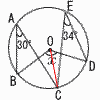７ (右図参照) 　∠x＝∠BOC＋∠COD 　　＝30×2＋34×2 　　＝60＋68＝128°

［トップに戻る］　［前ページに戻る］