| 1 |
(1) |
 6÷(-2)-4 6÷(-2)-4 |
5 |
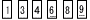 図のように,1,3,4,6,8,9の数字が1つずつ書かれた6枚のカードがある。この6枚のカードをよくきって,同時に2枚ひく。 図のように,1,3,4,6,8,9の数字が1つずつ書かれた6枚のカードがある。この6枚のカードをよくきって,同時に2枚ひく。 |
| (2) |
a+b+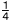 (a-8b) (a-8b) |
| (3) |
(x-2)2+3(x-1) |
(1) |
ひいた2枚のカードに善かれた数が,どちらも3の倍数である場合は何通りあるか求めなさい。 |
| 2 |
(1) |
5x2-5y2を因数分解しなさい。 |
| (2) |
x=√3+2,y=√3-2のとき,5x2-5y2の値を求めなさい。
|
(2) |
ひいた2枚のカードに書かれた数の積が,3の倍数である確率を求めなさい。
|
| 3 |
| 階級(回) |
度数(人) |
以上 未満
30~50 |
59 |
| 50~70 |
79 |
| 70~90 |
37 |
| 90~1100 |
40 |
| 110~130 |
25 |
| 計 |
240 |
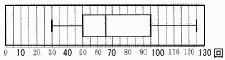
資料は.ある中学校の生徒240人のスポーツテストにおけるシャトルランの結果を表した度数分布表と箱ひげ図である。
 |
6 |
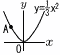 図のように,関数y= 図のように,関数y=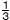 x2のグラフ上に点Aがあり,点Aのx座標は-3である。 x2のグラフ上に点Aがあり,点Aのx座標は-3である。
|
| (1) |
点Aのy座標を求めなさい。
|
| (1) |
90回以上110回未満の階級の相対度数を求めなさい。ただし,小数第3位を四捨五入して,小数第2位まで求めること。
|
(2) |
関数y=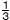 x2について,xの変域が-3≦x≦aのとき,yの変域が0≦y≦3となるような整数aの値をすべて求めなさい。 x2について,xの変域が-3≦x≦aのとき,yの変域が0≦y≦3となるような整数aの値をすべて求めなさい。
|
| (2) |
資料から読みとれることとして正しいものを,次のア~エのうちから1つ選び,符号で答えなさい。
| ア |
範囲は100回である。 |
イ
|
70回以上90回未満の階級の累積度数は102人である。 |
ウ
|
度数が最も少ない階級の階級値は120回である。 |
| エ |
第3四分位数は50回である。 |
|
|
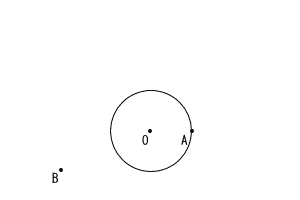
 下の図のように,円Oの円周上に点Aがあり,円0の外部に点Bがある。点Aを接点とする円Oの接線と点Bから円Oにひいた2本の接線との交点P,Qを作図によって求めなさい。なお,AP>AQであるとし,点Pと点Qの位置を示す文字PとQも書きなさい。 下の図のように,円Oの円周上に点Aがあり,円0の外部に点Bがある。点Aを接点とする円Oの接線と点Bから円Oにひいた2本の接線との交点P,Qを作図によって求めなさい。なお,AP>AQであるとし,点Pと点Qの位置を示す文字PとQも書きなさい。
ただし,三角定規の角を利用して直線をひくことはしないものとし,作図に用いた線は消さずに残しておくこと。
|
| 4 |
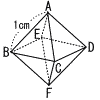 下の図のように,点A,B,C,D,E,Fを頂点とする1辺の長さが1cmの正八面体がある。 下の図のように,点A,B,C,D,E,Fを頂点とする1辺の長さが1cmの正八面体がある。 |
9 |
| (1) |
線分BDの長さを求めなさい。
|
| (2) |
正八面体の体積を求めなさい。
|
|

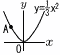 図のように,関数y=
図のように,関数y=
 下の図のように,点A,B,C,D,E,Fを頂点とする1辺の長さが1cmの正八面体がある。
下の図のように,点A,B,C,D,E,Fを頂点とする1辺の長さが1cmの正八面体がある。