|
正 答 2 | |||
| 9 栃木県 〜 16 富山県 |
|
正 答 2 | |||
| 9 栃木県 〜 16 富山県 |
| 9栃木県 | 1 3+5=8
3 x2+6x+9 4 7x+5y≦2000 5 4つ ねじれの位置とは,平行でない,交わらない辺 EH,FG,DH,CG 6 y= 8=a/(−2)で,a=−16
7 弧ACの中心角=360−134=226° ∠x=226÷2=113° 8 面積比は,32:52=9:25 よって, 25/9 倍 〜2番問題の一部 (おまけ)〜 1 解の公式より,
2 15x+34=20(x−2)+14 15x+34=20x−26 5x=60で, x=12 |
12千葉県 | 1 (1) −3−4=−7 (2) a+ (3) x2−4x+4+3x−3=x2−x+1 2 (1) 5(x+y)(x−y) (2) x+y=2√3,x−y=4 (1)より,与式=5×2√3×4=40√3 3 (1) 40÷240≒0.17 (2) ウ ア…範囲=125−30=95回(誤) イ…累積度数=59+79+37=175回(誤) エ…第3四分位数=95回(誤) 4 (1) 1辺1cmの正方形の対角線で, 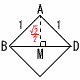 BD=√12+12=√2 BD=√12+12=√2(2) (右図参照) 高さAM=
(2) 6枚から2枚のひき方は,6×5÷2=15通り 3の倍数でないのは, (1,4) (1,8) (4,8) の3通り 3の倍数の確率=1−3の倍数でない確率 =1−3/15= 6 (1) y= 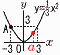 y= y=(2) (右図参照) 最大値は3だから,0≦a≦3 aは整数で, a=0,1,2,3 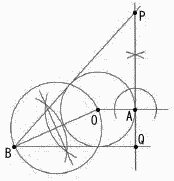 7 右図 7 右図・接点Aの接線を引く ・Bから円Oへ2本の 接線を引く ・交点P,Qをとる |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 10群馬県 | 【前期】 1 (1) −2 (2) 5×9=45 (3) −4a (4) 3x+4y−x+y=2x+5y (5) 3a−2b
2 xy+3x−y−3 3 (x−5)(x+3) 4 オ 5 y= −3=a/(−4)で,a=12
3x+2(x−3)=−1 5x=5で,x=1 これを下式に代入して, y=1−3=−2 よって, x=1,y=−2 7 ∠xの外角 =360−(80+80+60+70)=70 ∠x=180−70=110° |
13東京都 | 1 −8+36÷9=−8+4=−4
4 4x−7x=5−32 −3x=−27より, x=9 5 上式×4−下式より, 3y=−3で,y=−1 これを上式に代入して, 2x−3=1で,x=2 よって, x=2,y=−1 6 解の公式より,
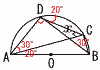 8 (右図参照) 8 (右図参照)∠DAC=∠DBC=30° ∠BDC=∠BAC=20° ∠x=180−(30+90+20)=40° 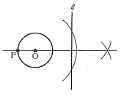 9 右図 9 右図・Oからl に垂線をおろす ・垂線と円周との交点(左側) をPとする |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 【後期】 1 (1) 2+4=6 (2) 2a3 (3) −6x+2y+2x=−4x+2y 2 (1) 6x−4x=−9+1 2x=−8で,x=−4 (2) 解の公式より,
4 座標を代入して,−12=a×(−2)2 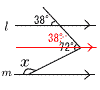 4a=−12で, a=−3 4a=−12で, a=−35 (右図参照) 平行線を引く 72−38=34° ∠x=180−34=146° 6 与式=(a−2)2=(2+√5−2)2 =(√5)2=5 7 2けたの数は,全部で4×3=12通り 32以上は,32,34,41,42,43の5通り 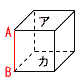 よって, 確率= よって, 確率=8 (右図参照) ア,カ 手前の面をイとすると,垂直は 上面アと,底面カ 9 イ,オ ア 最小値だが,1人とは限らない (誤) ウ 57回は中央値(誤) エ 57回以下は8人いるが, 9人目が60回以下とは限らない(誤) |
14神奈川県 | ア −1+7=6(答3)
=6+5√6(答2) 〜2番問題 (おまけ) ア x2−2x−15−2x+10=x2−4x−5 =(x−5)(x+1) (答2) イ 解の公式より,
100x+40+10−x =100(10−x)+40+x+396 198x=1386で, x=7(答2) オ 3780=22×33×5×7より, n=3×5×7=105(答3) |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 11埼玉県 | 1 4x 2 −28+20=−8
8x=24で, x=3
7 上式×2+下式×3より, 37y=37で,y=1 これを上式に代入して, 3x+5=2で,x=−1 よって, x=−1,y=1 8 解の公式より,
10 y=6/xにx=−6,2を代入して, 2点の座標は, A(−6,−1) B(2,3)
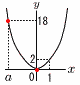 y= y=11(右図参照) x=1のとき,y=2×12=2 x=aのとき,最大値はy=18 18=2×a2より,a=−3 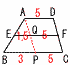 12(右図参照) 12(右図参照)AP//DCを引くと, △ABPで,EQ=1.5 EF=1.5+5=6.5cm (
全部で,23=8通り 100円以上は5通りで, 確率= 14(右図参照) 円の半径r=√72−42=√33 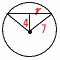 面積=(√33)2π=33πcm2 面積=(√33)2π=33πcm215 エ
ヒストグラムから読み取ることができる第3四分位数は,40分以上50分未満の階級に含まれているが,イの第3四分位数は50分以上60分未満で,異なっている。 |
15新潟県 | 1 7+3−3=7 2 6a−4b−8a+12b=−2a+8b
7y=35で,y=5 これを下式に代入して, 2x−5=7で,x=6 よって, x=6,y=5
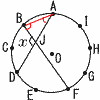 7 (右図参照) 7 (右図参照)∠BAD= = ∠ABF=40×2=80° △ABJで,∠x=40+80=120° 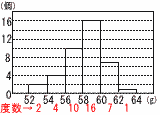 8 (右図参照) 8 (右図参照)四分位数を求める Q1=56〜58g (エは不適) Q2=58〜60g (イは不適) Q3=58〜60 g (ウは不適,アは適) よって, ア |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 16富山県 | 1 9−6=3
5 上式×2+下式×5より,
これを上式に代入して, 8+5y=−2で,y=−2 よって, x=4, y=−2 6 x−2=±5より,x=±5+2 よって, x=7,−3 7 a=8b+5 (a−8b=5等も可) 8 (右上表参照) 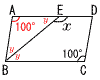 すべての目の出方は36通り すべての目の出方は36通りこのうち,差が3は6通り 確率=6÷36= 9 (右図参照) △ABEは二等辺三角形  ∠y=(180−100)÷2=40° ∠y=(180−100)÷2=40°∠x=180−40=140° 10 右図 ・弦を1本引く ・弦の垂直二等分線を引く |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| [トップに戻る] [前ページに戻る] [次ペ−ジに進む] |