| 【 A 】 |
| 1 |
(1) |
 3+(-6)-(-8) 3+(-6)-(-8)
|
6 |
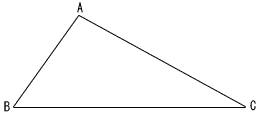
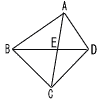  図のように,四角形ABCDがあり,対角線ACと対角線BDの交点をEとする。∠ABE=34°,∠BAD=90°,∠BCE=56°,∠BEC=80°であるとき,∠CDEの大きさは何度か。 図のように,四角形ABCDがあり,対角線ACと対角線BDの交点をEとする。∠ABE=34°,∠BAD=90°,∠BCE=56°,∠BEC=80°であるとき,∠CDEの大きさは何度か。
|
| (2) |
|
| (3) |
8a2b÷(-2a3b2)×(-3a)
|
| (4) |
|
7 |
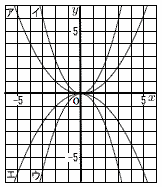
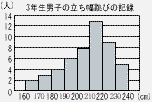 右のグラフは,ある中学校の3年生男子50人について,立ち幅とびの記録をヒストグラムで表したものである。このヒストグラムでは,例えば,立ち幅とびの記録が170cm以上180cm未満の男子生徒が3人いることがわかる。 右のグラフは,ある中学校の3年生男子50人について,立ち幅とびの記録をヒストグラムで表したものである。このヒストグラムでは,例えば,立ち幅とびの記録が170cm以上180cm未満の男子生徒が3人いることがわかる。
このヒストグラムにおいて,3年生男子50人をもとにした,立ち幅とびの記録が200cm以上230cm未満の生徒の人数の割合は何%か。
|
| 2 |
ある高校で,スキー研修に参加する生徒に対して,スキーの経験があるかどうかを調べたところ,男子a人のうちの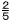 ,女子b人のうちの ,女子b人のうちの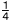 がスキーの経験があると答え,スキーの経験がある生徒の合計は35人であった。このとき,bをaの式で表しなさい。 がスキーの経験があると答え,スキーの経験がある生徒の合計は35人であった。このとき,bをaの式で表しなさい。
|
| 3 |
次の関数のうち,x>0の範囲において,xの値が増加するとyの値が減少する関数はどれか。次のア~エからすべて選び,その記号を書きなさい。
ア y=-3x イ y=-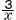
ウ y=x-3 エ y=-3x2
|
8 |
下の図のような,三角形ABCがある。2辺AB,ACから等しい距離にあり,2点A,Bから等しい距離にある点Pを,定規とコンパスを使い,作図によって求めなさい。ただし,定規は直線をひくときに使い,長さを測ったり角度を利用したりしないこととする。なお,作図に使った線は消さずに残しておくこと。 |
| 4 |
2次方程式 x2+2x-14=0 の解を求めなさい。ただし,「(x+▲)2=●」の形に変形して平方根の考え方を使って解き,解を求める過程がわかるように,途中の式も書くこと。
|
 |
| 5 |
 関数 y=3x2について,xの変域がa≦x≦1のとき,yの変域は0≦y≦12である。このときのaの値を求めなさい。 関数 y=3x2について,xの変域がa≦x≦1のとき,yの変域は0≦y≦12である。このときのaの値を求めなさい。
|

 右のグラフは,ある中学校の3年生男子50人について,立ち幅とびの記録をヒストグラムで表したものである。このヒストグラムでは,例えば,立ち幅とびの記録が170cm以上180cm未満の男子生徒が3人いることがわかる。
右のグラフは,ある中学校の3年生男子50人について,立ち幅とびの記録をヒストグラムで表したものである。このヒストグラムでは,例えば,立ち幅とびの記録が170cm以上180cm未満の男子生徒が3人いることがわかる。
 関数 y=−
関数 y=−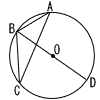 右の図のように,点A,B,C,Dは円Oの周上にあり,線分BDは円Oの直径,∠ABD=64°である。このとき,∠BCAの大きさは何度か。
右の図のように,点A,B,C,Dは円Oの周上にあり,線分BDは円Oの直径,∠ABD=64°である。このとき,∠BCAの大きさは何度か。