|
���@���@�T | |||
| 33�@���R���@�`�@40�@������ |
|
���@���@�T | |||
| 33�@���R���@�`�@40�@������ |
| 33���R�� | �P 2�{4��6 �Q �|8�|3���|11 �R 6a�|2b�|a�{5b��5a�{3b �S ����, 7ab�~b��7ab2 �T 1�{2��3�{3��4�{2��3 �U a(x2�|16)��a(x�{4)(x�|4)
�@�C,�E �X �A,�G 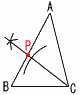 10 �E�} 2�������瓙�����̓_��, �@2�����̂Ȃ��p�̓����� �܂�,��ACB�̓�����ɂ��� �E��C�̓���������, �@AB�Ƃ̌�_��P�Ƃ��� |
38���Q�� | �P �|9
�@���|9�{5��5 �T (a2�|9)�{(a2�{10a�{15)��2a2�{10a�{15 �@�`�Q�Ԗ�� �i���܂��j�` 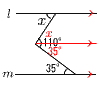 �P (5x�|1)(x�{1)��0���, �P (5x�|1)(x�{1)��0���, �@�@x�� �Q (�E�}�Q��) 110���s���œ��� ��x��110�|35��75�� �R�C |
|||||||||||||||||||||||||||||||||||||||
| 34�L���� | �P 3�{6��9 �Q 12x�{3y�|5x�{10y��7x�{13y �R 3��5�|��5�{2��5��4��5 �S y(x2�|4)��y(x�{2)(x�|2) 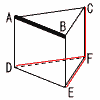 �T (�E�}�Q��) �T (�E�}�Q��)���s�łȂ�,�����Ȃ��ӂ�, �@CF, DF, EF �U y��
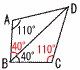 �V (�E�}�Q��) �V (�E�}�Q��)3�ӑ������,��ABD�߁�CBD ��ADC��360�|(110�{40)�~2 �@��360�|300��60�� �W 14��40��0.35 |
39���m�� | �@�y�@�`�@�z �P (1) 3�|6�{8��5
�@�ڍ�����, �@���ӂ�4�{����, b��140�| �R ���ꂼ��̃O���t��,���̒ʂ� 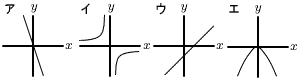 �@�����, �A,�G �S �ڍ�����,x2�{2x��14 �@���ӂ�1��������,x2�{2x�{1��14�{1 �@�@�@x2�{2x�{1��15 �@���ӂ�ό`����,(x�{1)2��15 �@���ӂ̕��������Ƃ���,x�{1���}��15 �@�ڍ�����, x���|1�}��15 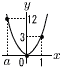 �T (�E�}�Q��) �T (�E�}�Q��)�ŏ��l��x��0�̂Ƃ���,y��0 x��1�̂Ƃ�,y��3�~12��3 �ő�l��y��12������,x��a�̂Ƃ� �@12��3x2��,x���}2 �@�Ƃ��낪,a��x��1������,a��0 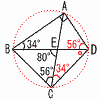 �����, a���|2 �����, a���|2�U (�E�}�Q��) ��ADB��90�|34��56�� ��ADB����ACB��56��������, �@ ��ACD����ABD��34��(��AD) ��CDE��,��CDE��80�|34��46�� �V (8�{13�{9)��50��0.6�@�����,60�� �W �E�} 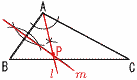 �E��A�̓���l ������ �E��A�̓���l �������E����AB�̐����� �@��m������ �El ��m�̌�_��P�Ƃ��� �@�y�@�a�@�z �P (1) 13�|9��4 �@(2) 7�|5�~4��7�|20���|13
�Q 2a�{3b��21 �@�ڍ�����,3b��21�|2a �@���ӂ�3�Ŋ�����, b��7�|
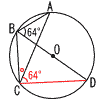 �R (x�{7)(x�|3)��0���, �R (x�{7)(x�|3)��0���, �@x���|7,3 �S x��3�̂Ƃ�,y���| �@�_(3,�|6)��ʂ�O���t��, �E �T (�E�}�Q��) ��ACD����ABD��64��(��AD) ��BCD��90��������, �@��BCA��90�|64��26��  �U (�E�\�Q��) �U (�E�\�Q��)a�{b��3,6,9,12�ƂȂ�o���� �@�E�\���,12�ʂ�
|
|||||||||||||||||||||||||||||||||||||||
| 35�R���� | �P 8�{5��13
�S 6x�{y�|9x�|7y���|3x�|6y �T a2�|9 �@�`�Q�Ԗ�� �i���܂��j�` �P y��3x�{7 �Q 10�Ԗڂ�����200�`300�l�̊K����, �C �R �����̖�������x�Ƃ����, �@���,4��x��5 �@���������Ƃ��,��16����x����25�c�A �A���,x2��18, �܂�x����18�c�C �A,�C���, x����17�@�@ |
|||||||||||||||||||||||||||||||||||||||||
| 36���쌧 | �P �|15�{9���|6 �Q 5x�|10y�|4x�|y��x�|11y �R 6a2��2a�|4ab��2a��3a�|2b �S ��16�|��8�{��2�|1��3�|��2 �T 3(x2�|4)��3(x�{2)(x�|2) �U x�|2���}��5��, x��2�}��5 �V �G �@�`�Q�Ԗ�� �i���܂��j�` 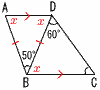 �P (�E�}�Q��) ��BAD�͓ӎO�p�`��, �@��px����A����B �@�@��(180�|50)��2��65�� AD//BC���, �@��ADB����DBC��65��(���p) ��DBC��,��C��180�|60�|65��55�� 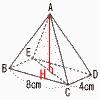 2 (1) �C 2 (1) �C�@(2) (�E�}�Q��) A������BCDE�� �@����AH�����낷 ��ACE�͓ӎO�p�`��, �@CE����82�{42��4��5cm ��ACE�� �@AH��60��4��5��3��5 �l�p������ |
|||||||||||||||||||||||||||||||||||||||||
| 37������ | �P �|7�{3���|4 �Q ����,3(5x�|2y)��15x�|6y �R ��25����30����36������,5����30��6 ��30��5.***��, a��5 �S 3�Ŋ�����,x2�|12��0 �@x2��12���, x���}��12���}2��3 �T 6a�{b��800 �U y��
�V ���_�����ɕ��בւ����, �@5,7, 7 ,8,10, 11 ,13,14, 16 ,19,20 �l���ʐ����, a��7,b��16  �W x:9��8:(20�|8)��8:12 �W x:9��8:(20�|8)��8:12�@12x��72��, x��6 �X �a���f���ɂȂ�o���� �@�E��\�̏ꍇ��,15�ʂ�
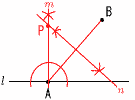 10 �E�} 10 �E�}�EA����l �̐���m������ �EAB�̐�������n �@�@������ �Em��n�̌�_�𒆐SO �@�@�Ƃ��� |
40������ | �P 6�|15���|9 �Q 3a�|12b�|2a�|5b��a�|17b �R ��9�{��7��3�{��7 �S x2�|4��x�{8 �@x2�|x�|12���O �@(x�|4)(x�{3)��0���, x��4,�|3 �T y��
�@�@5�~4��2��10�ʂ� [3]���܂܂��̂�,����4�ʂ� �@(3,1) (3,2) (3,4) (3,5)
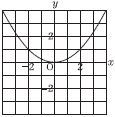 �V �E�} �V �E�}�W (6�{9�{17)��60��32��60 �@��0.533�c ��0.53 �X �˂��̑�����x�Ƃ����,
|
| �m�g�b�v�ɖ߂��n�@�m�O�y�[�W�ɖ߂��n�@�m���y�|�W�ɐi���n |