| １ |
(1) |
 3－7
|
６ |
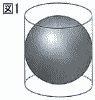 図1のように,底面の直径と高さが等しい円柱の中に,直径が円柱の高さと等しい球が入っている。このとき,球の体積は円柱の体積の何倍か。
|
| (2) |
4(x＋2)＋2(x－3)
|
| (3) |
12x2y÷4x2×3xy
|
７ |
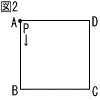 図2のような正方形ABCDがあり,点Pが頂点Aの位置にある。2つのさいころを同時に1回投げて,出た目の数の和と同じ数だけ,点Pは頂点B,C,D,A,B,…の順に各頂点を反時計回りに1つずつ移動する。例えば,2つのさいころの出た目の数の和が5のとき,点Pは頂点Bの位置に移動する。
2つのさいころを同時に1回投げたとき,点Pが頂点Dの位置に移動する確率を求めよ。
|
| (4) |
(x＋2)(x＋8)－(x＋4)(x－4)
|
| ２ |
2次方程式 x2－6x＋2＝0 を解け。
|
| ３ |
x＝√2＋3のとき, x2－6x＋9 の値を求めよ。
|
８ |
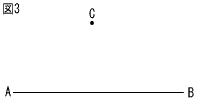
 図3のように線分ABと点Cがある。線分AB上にあり,∠APC=45°となる点Pを,定規とコンパスを使って作図せよ。なお,作図に使った線は消さずに残しておくこと。 |
| ４ |
yはxの2乗に比例し,x＝2のときy＝－8である。yをxの式で表せ。
|
|
| ５ |
| 階級(分) |
度数(人) |
以上未満
5～10 |
2 |
| 10～15 |
5 |
| 15～20 |
10 |
| 20～25 |
6 |
| 25～30 |
8 |
| 30～35 |
6 |
| 35～40 |
2 |
| 40～45 |
1 |
| 計 |
40 |
右の表は,ある学級の生徒40人の通学時間を度数分布表に整理したものである。中央値（メジアン）が含まれる階級の相対度数を求めよ。
|
印刷用