| 【 B 】 |
| 1 |
(1) |
 -4-(-3)+6 -4-(-3)+6
|
5 |
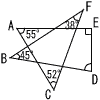 右の図で,∠A=55°,∠B=45°,∠C=52°,∠E=90°,∠F=38°である。このとき,∠Dの大きさは何度か。 右の図で,∠A=55°,∠B=45°,∠C=52°,∠E=90°,∠F=38°である。このとき,∠Dの大きさは何度か。
|
| (2) |
 32-6÷(-2) 32-6÷(-2)
|
| (3) |
-5b2÷10ab×4a
|
6 |
1枚の硬貨を4回続けて投げるとき,硬貨の表と裏が2回ずつ出る確率を求めよ。ただし,硬貨は表と裏のどちらが出ることも同様に確からしいものとする。
|
| (4) |
15÷√5+√20
|
| 2 |
a%の食塩水600gの中に溶けている食塩の量をbgとする。このとき,bをaの式で表せ。
|
2番問題 ~ おまけ ~
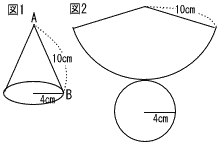
次の図1は,底面の半径が4cm,母線ABの長さが10cmの円すいであり,図2は,図1の円すいの展開図である。ただし,円周率はπを用いること。
|
| 3 |
| 方程式 |
x |
+ |
y |
=1のグラフを,次のア~エから |
| 2 |
3 |
1つ選び,その記号を書け。
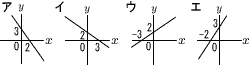
|
| 4 |
関数y=−2x2において,xの値とそれに対応するyの値について述べた文として正しいものを,次のア~エから1つ選び,その記号を書け。ただし,xは0でないものとする。
ア
|
xの値を2倍,3倍,4倍にすると,対応するyの値はそれぞれ2倍,3倍,4倍となる。 |
イ
|
xの値を2倍,3倍,4倍にすると,対応するyの値はそれぞれ-2倍,-3倍,-4倍となる。 |
ウ
|
xの値を2倍,3倍,4倍にすると,対応するyの値はそれぞれ4倍,9倍,16倍となる。 |
エ
|
xの値を2倍,3倍,4倍にすると,対応するyの値はそれぞれ-4倍,-9倍,-16倍となる。 |
|
1 |
図2において,おうぎ形の中心角の大きさは何度か。
|
| 2 |
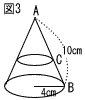 図3のように,図1の円すいを底面に平行な平面で切断したときの母線ABとの交点をCとする。ACを母線とする円すいの側面積が,ABを母線とする円すいの側面積の半分となるとき,ACの長さを求めよ。 図3のように,図1の円すいを底面に平行な平面で切断したときの母線ABとの交点をCとする。ACを母線とする円すいの側面積が,ABを母線とする円すいの側面積の半分となるとき,ACの長さを求めよ。
|
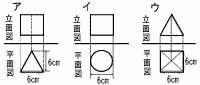
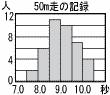 右のグラフはある中学校の3年生女子40人について,50m走の記録をヒストグラムで表したものである。このヒストグラムでは,例えば,50m走の記録が8.0秒以上8.5秒未満の女子が6人いることがわかる。
右のグラフはある中学校の3年生女子40人について,50m走の記録をヒストグラムで表したものである。このヒストグラムでは,例えば,50m走の記録が8.0秒以上8.5秒未満の女子が6人いることがわかる。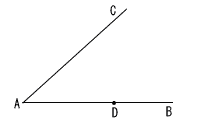
 右の図で,∠A=55°,∠B=45°,∠C=52°,∠E=90°,∠F=38°である。このとき,∠Dの大きさは何度か。
右の図で,∠A=55°,∠B=45°,∠C=52°,∠E=90°,∠F=38°である。このとき,∠Dの大きさは何度か。
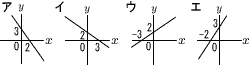
 図3のように,図1の円すいを底面に平行な平面で切断したときの母線ABとの交点をCとする。ACを母線とする円すいの側面積が,ABを母線とする円すいの側面積の半分となるとき,ACの長さを求めよ。
図3のように,図1の円すいを底面に平行な平面で切断したときの母線ABとの交点をCとする。ACを母線とする円すいの側面積が,ABを母線とする円すいの側面積の半分となるとき,ACの長さを求めよ。