|
���@���@�T | |||
| 33�@���R���@�`�@40�@������ |
|
���@���@�T | |||
| 33�@���R���@�`�@40�@������ |
| 33���R�� | �P �|3�{7��4 �Q �|20 �R 3a�|6b�|2a�|2b��a�|8b �S �|5ab �T 7�|5��2 �U ���̌������,
�W �a��5�ȉ���,����10�ʂ� �@(��,��)��(1,1) (1,2) (2,1) (1,3) (2,2) �@�@�@(3,1) (1,4) (2,3) (3,2) (4,1) �@�����, �m����10/36��5/18 �X �O�����̒藝���, �@AO2+32��72��,AO��2��10
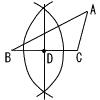 �@�@��6��10��cm3 �@�@��6��10��cm310 �E�} �@����AD���Ƃ�悢 �@�܂�,��BC�̒��_��D �@ |
38���Q�� | �P �|15�@�@�@�Q
�T (x2�|6x�{9)�|(x2�|16) �@���|6x�{25 �@�`�Q�Ԗ��̈ꕔ �i���܂��j�` �P (x�|2)(x�|6)
�@�E, �G �S 13�l�̒����l��7�Ԗڂ�,26m �@14�l�̒����l��7�Ԗ�(26m)�� �@�@�@8�Ԗ�(x�Ƃ���)�̕��ς�, �@(26�{x)��2��26�{1 �@x��27�~2�|26��54�|26��28m |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 34�L���� | �P 6�|5�{2��3 �Q �^����2a��2�~4��8
�T �U ��(3�|1)2�{(2�|7)2����4�{25����29 �V �@ �C�@�A �A�@�B �E 8 �a��6�ȏ�ɂȂ�̂�,����3�ʂ� �@(A,B)��(3,3) (4,2) (4,3)
|
39���m�� | �@�y�@�`�@�z �P (1) 2�{5�|9���|2
�R �A,�E,�G �S x2�|2x�|8��3x�|2 �@x2�|5x�|6��0 �@(x�|6)(x�{1)��0���, x��6,�|1 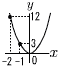 �T (�E�}�Q��) �T (�E�}�Q��)�@y��ax2��(�|1,3)��������, �@3��(�|1)2a��, a��3 �U �E,�A,�C �@���������Ƃ���Ƒ̐ς� �@�@�A�� �@�@�C��32���~h��28.3h �@�@�E�� �V �f�[�^�͏���������, 2,6,11,10,7,4�l �@�����l��20�21�Ԗڂ�,9.0�`9.5�b�̊K�� �@�����, ���Γx����10��40��0.25 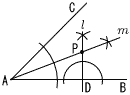 �W �E�} �W �E�}�ED����AB�̐���l ���Ђ� �E��A�̓���m���Ђ� �El ��m�̌�_��P�Ƃ��� �@�y�@�a�@�z �P (1) �|4�{3�{6��5 �@ (2) 9�{3��12
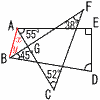 �S �E �S �E�@y��x��2��ɔ�Ⴕ, �@�@���萔�́|2 �T (�E��}�Q��) AB������ �@��GAB�Ɓ�FGC�� �@�@x�{y��38�{52��90�� �@��D��360�|(90�{55�{45�{90)��80��  �U �E�̎��`�}���, �U �E�̎��`�}���,�@�@�����ɍ����̂�����6�ʂ� �@�m����6��24�� �@�`�Q�Ԗ�� �i���܂��j�` �P �������`�̌ʁ���ʂ̉~�� �@�@��8�� �@���S�p��x�Ƃ����,
�Q ���~�������~���� �@�ʐϔ䂪1:2������,�������1:��2
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 35�R���� | �P 2 �Q �|6 �R 10a�|6a�|8��4a�|8 �S 3b �T 6x�|3y�{4x�{12y��10x�{9y �@�`�Q�Ԗ�� �i���܂��j�` �P �� �Q �G �R y�� �@2��a/3���, a��6 �@�����, y�� �S ������h�Ƃ����, �@�̐ρ� �@h��96�~3��36��8cm �@ |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 36���쌧 | �P 2�{5�|4��3 �Q 3�~4�~(�|4)���|48 �R ���ӂ�3�Ŋ�����,4x�|y��2 �@���E�̕ӂ����ւ���,2��4x�|y �@2�Ɓ|y���ڍ�����, y��4x�|2
�T xy�{y�|6x�|6��(x�{1)y�|6(x�{1) �@��(x�{1)(y�|6) �U ���̌������,
�V �C,�E,�A �@�`�Q�Ԗ��̈ꕔ �i���܂��j�` 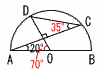 1(�E�}�Q��) 1(�E�}�Q��)�@��AOD��90�|20��70�� �@��ACD��70��2��35�� �@ |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 37������ | �P �|3 �Q ��24��2��6 �R x2�|9x�{20 �S ���̌������,
�@�����,���Γx����12��30��0.4 �V ��A��110����E��100�� �@�܊p�`�̓��p�̘a��180�~3��540�� �@�����,��B��540�|(110�{105�{110�{100 �@�@�@��540�|425��115�� �W y�� �@3�� �@�@����y�� �X ��������172�|32����40��2��10
�@ |
40������ | �P 7�|12���|5 �Q 6a�{3b�|8a�{10b���|2a�{13b
�@�@x2�|8x�|20��0 �@�@(x�|10)(x�{2)��0���, x��10,�|2 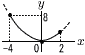 �T �]���ۂ̊m���𗘗p �T �]���ۂ̊m���𗘗p�@(���Ȃ��Ƃ�1���͕\�̊m��) �@�@��1�|(4���Ƃ����̊m��)
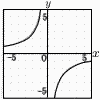 �@�ő�l�� �@�ő�l���@�ŏ��l�� �@�����, 0��y��8 �V �E�O���t �W (�E�}�Q��) �X (�E���}�Q��) ��ABC��(180�|48)��2��66�� 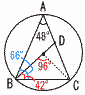 ��BOC��96�����,��DBC��42�� ��BOC��96�����,��DBC��42����ABD��66�|42��24�� ��ABD�� �@��ADB��180�|(48�{24)��108�� |
| �m�g�b�v�ɖ߂��n�@�m�O�y�[�W�ɖ߂��n�@�m���y�|�W�ɐi���n |