| 1 番 問 題 |
2番問題 ~おまけ~ |
| 1 |
(1) |
 18÷(-6)-9 18÷(-6)-9
|
1 |
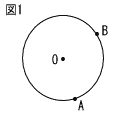
 図1において,2点A,Bは円Oの円周上の点である。∠AOP=∠BOPであり,直線APが円Oの接線となる点Pを作図しなさい。 図1において,2点A,Bは円Oの円周上の点である。∠AOP=∠BOPであり,直線APが円Oの接線となる点Pを作図しなさい。
ただし,作図には定規とコンパスを使用し,作図に用いた線は残しておくこと。 |
| (2) |
(-2a)2÷8a×6b
|
| (3) |
|
 |
| (4) |
(√5+√3)2-9√15
|
2 |
1から3までの数字を1つずつ書いた円形のカードが3枚,4から9までの数字を1つずつ書いた六角形のカードが6枚,10から14までの数字を1つずつ書いた長方形のカードが5枚の,合計14枚のカードがある。図2は,その14枚のカードを示したものである。
1から6までの目がある1つのさいころを2回投げ,1回目に出る目の数をa,2回目に出る目の数をbとする。
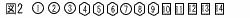 |
| 2 |
a=11,b=43のとき,16a2-b2 の式の値を求めなさい。
|
(1) |
14枚のカードに書かれている数のうち,小さい方からa番目の数と大きい方からb番目の数の和を,a,bを用いて表しなさい。
|
| 3 |
次の2次方程式を解きなさい。
(x-2)(x-3)=38-x
|
(2) |
 14枚のカードから,カードに書かれている数の小さい方から順にa枚取り除き,さらに,カードに書かれている数の大きい方から順にb枚取り除くとき,残ったカードの形が2種類になる確率を求めなさい。ただし,さいころを投げるとき, 1から6までのどの目が出ることも同様に確からしいものとする。 14枚のカードから,カードに書かれている数の小さい方から順にa枚取り除き,さらに,カードに書かれている数の大きい方から順にb枚取り除くとき,残ったカードの形が2種類になる確率を求めなさい。ただし,さいころを投げるとき, 1から6までのどの目が出ることも同様に確からしいものとする。
|
