|
正 答 3 | |||
| 17 石川県 ~ 24 三重県 |
|
正 答 3 | |||
| 17 石川県 ~ 24 三重県 |
| 17石川県 | 1 (1) 6+1=7 (2) 4-15=-11
3 各辺を2乗すると,16<n<25 n=17,18,19,…,24で, 8個 4 底面=32π=9π 半球面=4π×32÷2==18π よって, 表面積=9π+18π=27πcm2 5 ウ 最頻値は,4人の1匹 平均値=(1×4+2+3×3+4+5)÷12 =24÷12=2匹 中央値は,6番目と7番目の平均値で, (1+2)÷2-1.5匹 範囲=5-0=5匹 |
22静岡県 | 1 (1) -3-9=-12
2 与式=(4a+b)(4a-b) =(4×11+43)(4×11-43) =87×1=87 3 x2-5x+6-38+x=0 x2-4x-32=0 (x+4)(x-8)=0より, x=-4,8 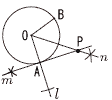 ~2番問題(おまけ)~ 1 右図 ・OとAを結ぶ直線l をかく ・Aを通るl の垂線mをかく ・∠AOBの二等分線nをかく ・直線mとnの交点をPとする 2 (1) 大きい方からb番目は15-b よって, a+(15-b)=a-b+15 (2) a=1,2のとき,b=1,2で,2×2=4通り a=3~6のとき,b=1~4で,4×4=16通り
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 18福井県 | 【 選択A 】
3 a2-22=(a+2)(a-2) 4 x2-4x+4+x2-6x+8=0 2x2-10x+12=0 2(x2-5x+6)=0 2(x-2)(x-3)=0より, x=2,3 5 2,3,5,7,11,13 6 y=-x2の式に値を代入 x=-2のとき,a=-(-2)2=-4 y=-9のとき,-9=-b2で,b=3 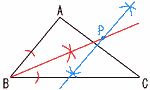 7 右図 7 右図【 選択B 】
3 選択Aの4と同じ [別解] 共通因数(x-2)でくくり出すと (x-2){(x-2)+(x-4)}=0 (x-2)(2x-6)=0 2(x-2)(x-3)=0より, x=2,3 4 400人の通学時間で,200番目と 201番目の値の平均をとる 5 イ, エ 6 2,3,5,7,11,13 7 余りは1 (説明) m,nが整数のとき, 6で割ると5余る数は, 6m+5 3で割ると2余る数は, 3n+2 と表せるから, 和=(6m+5)(3n+2) =18mn+12m+15n+10 =3(6mn+4m+5n+3)+1 6mn+4m+5n+3も整数だから 和=3×(整数)+1で, 余りは1 8 選択Aの7と同じ |
23愛知県 | 【 A 】 1 5+3=8
5 連続3数をx,x+1,x+2とすると, x2+(x+1)2+(x+2)2=365 x2+(x2+2x+1)+(x2+4x+4)=365 3x2+6x+5=365 移項して,3で割ると, x2+2x-120=0 (x-10)(x+12)=0 xは自然数だから, x=10 6 ウ,エ ア y=x3 (3次関数) イ y=50/x (反比例) ウ y=2πx (1次関数) エ y=0.05x (1次関数) 7 余事象の確率で考える (少なくとも1人はあたる確率) =1-(2人ともはずれる確率)で, 確率=1- 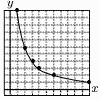 8 (右グラフ参照) 6個 8 (右グラフ参照) 6個比例定数a= 式はy=12/x 9 連立方程式を解く
5x=10より,x=2 これを上式に代入して, y=3×2-5=1 よって, 交点は(2,1) 10 △OBCは正三角形で, BC=6cm |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 19山梨県 | 1 -21 2 3 -16+49=33 4 √20+√5=2√5+√5=3√5 5 -7x 6 6x+7y-2x-6y+18=4x+y+18 ~2番問題(おまけ)~ 1 (x+2)(x-9)=0より, x=-2,9 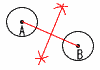 2 右図 2 右図・線分ABの垂直二等分 線を引けばよい 3 ∠A=∠D=52° ∠CEB=∠A+∠C =52+43=95°
|
【 B 】 1 3-7×(-3)=3+21=24
4 x2-2x-8=(x-4)(x+2) 5 x+2=±√7より, x=-2±√7 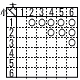 6 a=10b+c 6 a=10b+c7ア,エ イ 中央値は49.5回 ウ 最頻値は45回 8 (右表参照) 9÷36= 9 y=6x+5の変化の割合(傾き)は6 y=ax2の変化の割合は,
AB:AC=AC:ADだから,6:5=5:AD 6AD=5×5で, AD=25/6 cm |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 20長野県 | 1 -4 2 ウ 3 5√2-2√2=3√2 4 x2+4x-2=0 解の公式より,
5 ウ,エ 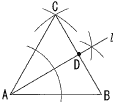 6 右図 6 右図・AB=ACとなる点Cをとる ・∠BACの二等分線l をひく ・BCとの交点をDとする 7 イ 8 子どもの人数 9 1番目の学さんの確率は 2番目の春さんの確率は
11 ∠x=(360-148)÷2=106° 12 △ADE∽△CBE(相似比1:2) DE:BE=1:2だから,BE=xとすると (12-x):x=1:2で,x=2(12-x) x+2x=24より, x=8cm |
24三重県 | 【 前 期 】 1 4-18=-14
4 上式×2+下式×3より, 17x=-34で,x=-2 これを上式に代入して, -8+3y=1で,y=3 よって, x=-2,y=3
(x-1)(x-9)=0で, x=1,9 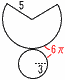 7 ア,エ 7 ア,エ8 (右図参照) 扇形の弧=底面の円周=6π 表面積=側面積+底面積 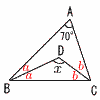 = ==15π+9π=24πcm2 9 (右図参照) 70+2(a+b)=180より, a+b=110÷2=55 ∠x=180-(a+b)=180-55=125° 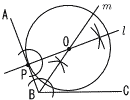 10 右図 10 右図・Pから垂線l をひく ・∠Bの二等分線mをひく ・l とmの交点をOとする ・Oを中心に, 半径OP(OB)の円をかく 【 後 期 】 1 8-13=-5 2 - 3 2x+6y-6x+9y=-4x+15y 4 6+3√10-√10-5=1+2√10 5 (x+3)(x-4) 6 解の公式より,
Aの相対度数=18÷50=0.36 Bの相対度数=28÷80=0.35 |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 21岐阜県 | 1 5-9=-4
x=6, 0 4 エ 中央値は6番目で,2点 最頻値は最多の,1点 平均値は,20÷11≒1.8点 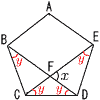 5 (右図参照) 5 (右図参照)△CBDと△DCEは 二等辺三角形 頂角=180-360÷5=108° y=(180-108)÷2=36 △CDFで, x=2y=2×36=72 6 図1の水の体積= 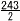 図2の水の体積=92x=81x 81x= 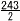 より, x= より, x=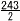 ÷81= ÷81=~2番問題(おまけ)~ 1 y=4000/x 2 y=4000/600= ~3番問題(おまけ)~ 1 6×6=36通り 2 (a,b)=(1,1) (1,2)…(1,6) の6通り 確率=6÷36= 3 できないのは,a=1かb=1の時 (a,b)=(1,1) (1,2) … (1,6) (2,1) (3,1) … (6,1) の11通り 確率=11/36 |
| [トップに戻る] [前ページに戻る] [次ペ-ジに進む] |