| 後 期 |
| 1 |
(1) |
 2-(-5) 2-(-5)
|
7 |
あるクラスの女子生徒20人が体力テストで反復横とぴを行い,その記録を整理したところ,20人の記録の中央値は50回であった。この20人の記録について,次のア~エのうち,必ず正しいといえるものを1つ選ぴ,記号で答えなさい。
| ア |
20人の記録の合計は,1000回である。 |
| イ |
20人のうち,記録が50回であった生徒が最も多い。 |
ウ
|
20人のうち,記録が60回以上であった生徒はl人もいない。 |
エ
|
20人のうち,記録が50回以上であった生徒が少なくとも10人いる。 |
|
| (2) |
 4x-2x× 4x-2x×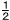
|
| (3) |
 -6a3b2÷(-4ab) -6a3b2÷(-4ab)
|
| 2 |
x=-2,y=3のとき,(2x-y-6)+3(x+y+2) の値を求めなさい。
|
8 |
2つの容器A,Bに牛乳が入っており,容器Bに入っている牛乳の量は,容器Aに入っている牛乳の量の2倍である。容器Aに140mLの牛乳を加えたところ,容器Aの牛乳の量と容器Bの牛乳の量の比が5:3となった。はじめに容器Aに入っていた牛乳の量は何mLであったか,求めなさい。
ただし,解答用紙の(解)には,答えを求める過程を書くこと。
|
| 3 |
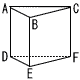 右の図の三角柱ABC-DEFにおいて,辺ABとねじれの位置にある辺を,すべて答えなさい。 右の図の三角柱ABC-DEFにおいて,辺ABとねじれの位置にある辺を,すべて答えなさい。
|
| 4 |
nを自然数とする。√24nが自然数となるようなnのうち,最も小さい数を求めなさい。
|
9 |
次の図のように,長い斜面にボールをそっと置いたところ,ボールは斜面に沿って転がり始めた。ボ-ルが斜面上にあるとき,転がり始めてからx秒後までにボ-ルが進んだ距離をymとすると,xとyの間には,y=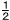 x2という関係が成り立っていることが分かった。 x2という関係が成り立っていることが分かった。
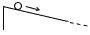 この関数について,xの値が1から3まで増加するときの変化の割合を調べて分かることとして,次のア~エのうち正しいものを1つ選び,記号で答えなさい。 この関数について,xの値が1から3まで増加するときの変化の割合を調べて分かることとして,次のア~エのうち正しいものを1つ選び,記号で答えなさい。
ア
|
変化の割合は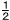 なので,1秒後から3秒後までの間にボールが進んだ距離は なので,1秒後から3秒後までの間にボールが進んだ距離は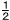 mである。 mである。 |
イ
|
変化の割合は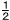 なので,1秒後から3秒後までの間のボールの平均の速さは秒速 なので,1秒後から3秒後までの間のボールの平均の速さは秒速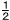 mである。 mである。 |
ウ
|
変化の割合は2なので,1秒後から3秒後までの間にボールが進んだ距離は2mである。 |
エ
|
変化の割合は2なので,1秒後から3秒後までの間のボールの平均の速さは秒速2mである。 |
|
| 5 |
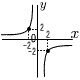 右の図の双曲線は,ある反比例のグラフである。この反比例について,yをxの式で表しなさい。 右の図の双曲線は,ある反比例のグラフである。この反比例について,yをxの式で表しなさい。
|
| 6 |
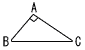 右の図のような∠A= 90°の直角三角形ABCにおいて,AB=2cm,CA=3cmである。辺BCの長さを求めなさい。 右の図のような∠A= 90°の直角三角形ABCにおいて,AB=2cm,CA=3cmである。辺BCの長さを求めなさい。
|

 右の図の三角柱ABC-DEFにおいて,辺ABとねじれの位置にある辺を,すべて答えなさい。
右の図の三角柱ABC-DEFにおいて,辺ABとねじれの位置にある辺を,すべて答えなさい。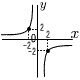 右の図の双曲線は,ある反比例のグラフである。この反比例について,yをxの式で表しなさい。
右の図の双曲線は,ある反比例のグラフである。この反比例について,yをxの式で表しなさい。 右の図のような∠A= 90°の直角三角形ABCにおいて,AB=2cm,CA=3cmである。辺BCの長さを求めなさい。
右の図のような∠A= 90°の直角三角形ABCにおいて,AB=2cm,CA=3cmである。辺BCの長さを求めなさい。