|
���@���@�Q | |||
| �X�@�Ȗ،��@�`�@16�@�x�R�� |
|
���@���@�Q | |||
| �X�@�Ȗ،��@�`�@16�@�x�R�� |
| �X�Ȗ،� | �P �|3�{7��4�@�@�Q 2ab2 �R �^����2�{(�|3)2��1�{9��11 �S (x�|4)2 �T ���Ӂ~5���,5a��2b�|c �@�ڍs����, c���|5a�{2b �U �A �@�C��16��4 �@�E��5�{��7����5�{7����12 �@�G(��2�{��6)2��8�{4��3 �@�@(��2)2�{(��6)2��8 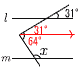 �V (�E�}�Q��) ���s�����Ђ� �V (�E�}�Q��) ���s�����Ђ��@��x��180�|64��116�� �W y�� �@6��a/3���, a��18 �@�����, y��18/x
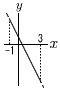 11 (�E�}�Q��) 11 (�E�}�Q��)�@x���|1�̂Ƃ�, �@�@y���|2�~(�|1)�{1��3 �@x��3�̂Ƃ�, �@�@y���|2�~3�{1���|5 �@�����, �|5��y��3
|
13�����s | �P �|9�~
�S �|4x�{2��9x�|63 �@�|13x���|65���, x��5 �T �㎮�~6�|�������, �@31x���|31��,x���|1 �@������㎮�ɑ������, �@�@�|5�{y��1��, y��6 �@�����, x���|1, y��6 �U x�{8���}��2���, x���|8�}��2 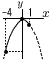 �V �@ �A�@�@�A �I �V �@ �A�@�@�A �I(�E�}�Q��) �@x���|4�̂Ƃ�, �@�@y���|3�~(�|4)2���|48(�ŏ��l) �@x��0�̂Ƃ�,y���|3�~02��0 (�ő�l)
�@a��b�ƂȂ�̂�,�E�\�́���, �@�@���̊m����21/36�� �X ���} 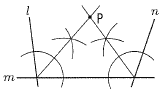 �@2�{��,�p�̓����̌�_��P |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 10�Q�n�� | �y�O���z �P (1) �|5�@�@(2) 8�|4��4��8�|1��7 �@ (3) �|25a�@�@(4) 2x �@ (5) 2a�{2b�|3a�{3b���|a�{5b �@ (6) 4��3�|��3��3��3 �Q 4a2�|4ab�{b2 �R (x�{6)(x�|7) �S 62���~(45/360)��36���~ �T y��2(x�{3)�|1��, y��2x�{5 �U �E,�I �V 6��38��0.1578�c��0.16 |
14�_�ސ쌧 | �A �|9�{5���|4 (���Q)
�@�`�Q�Ԗ�� �i���܂��j�` �A x�{6��A�Ƃ����, �@�^����A2�|5A�|24��(A�|8)(A�{3) �@�@��(x�{6�|8)(x�{6�{3) �@�@��(x�|2)(x�{9)�@�@ (���S) �C ���̌������,
�G 15x�{9y��200 (���P)
�@��DCE��180�|(40�{34)��106�� 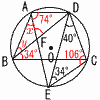 �@��DAF��180�|��DCE��74�� �@��DAF��180�|��DCE��74���@��DBC����E��34�� �@AD//BC���,��A�{��B��180�� �@�@(x�{74)�{(y�{34)��180 �@��AFD��x�{y �@�@��180�|(74�{34)��72�� (���P)�@ |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| �y����z �P (1) 2�{5��7�@�@(2) 4x�|x��3x �@ (3) �Q �^����2x�|y�|6�{3x�{3y�{6 �@�@�@��5x�{2y��5�~(�|2)�{2�~3 �@�@�@���|10�{6���|4 �R ���s�łȂ�,�����Ȃ��ӂ�����, �@��CF, ��DF, ��EF �S ��24n��2��6��n���, n��6 �T y�� �@�|2��a/2��, a���|4 �@�����, y���| �U BC����22�{32����13cm �V �G �@�����l50���,20�E21�Ԗڂ̋L�^ �W �͂��߂̋�����xmL�Ƃ����, �@�@(x�{140):2x��5:3 �@�@3(x�{140)��2x�~5 �@�����������,x��60 �@�@�@(��)�@60mL �X �G
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 11��ʌ� | �P �|5x�@�Q �|3�|20���|23
�@�@�|2x���|8��, x��4
�U (x�|2)(x�{9) �V �㎮�~3�|�����~4���, �@7x��7��,x��1 �@����������ɑ������, �@�@2�|3y��5��,y���|1 �@�����, x��1,y���|1 �W ���̌������,
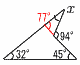 �X (�E�}�Q��) �X (�E�}�Q��)�@x��(32�{45)�|77��17�� 10 (�E���}�Q��) �@�ő�l��x��0�̂Ƃ���0 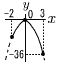 �@�ŏ��l��x��3�̂Ƃ��� �@�ŏ��l��x��3�̂Ƃ����@�@a�~32���|36���, a���|4 11������r��2��������
12 �C 13 �A 1.27�@�@�C 4 �@12700��1.27�~10000��1.27�~104 14 �G �P�T �����l��20�21�Ԗڂ� �@�@6�`8���Ԃ̊K��������,14�l �@�����, 14��40��0.35 �P�U 4�~4�|4�~3��4 (cm) |
15�V���� | �P �|7 �Q 6a�{2b�|a�|4b��5a�|2b
�S 2��7�{��7��3��7 �T ���̌������,
�U y��ax2��,(�|2,12)��������, �@12��a�~(�|2)2���,a��3 �@�����, y��3x2 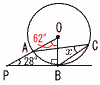 �V (�E�}�Q��) �@��OPA��,��OBP��90�����, �@�@��POB��180�|(28�{90)��62�� �@��x�� �W �@(1)�@20��80��0.25 �@(2)�@�����l��(40�Ԗځ{41�Ԗ�)��2 �@�@�@�@40�E41�Ԗڂ͂Ƃ��� �@�@�@�@�@600m�ȏ�`800m���� �̊K�� |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 12��t�� | �P 40�@�@�Q �|9�{(�|2)���|11 �R 8a�|5b�|2a�{3b��6a�|2b �S �㎮�{�����~3���, �@11x���|44��,x���|4 �@����������ɑ������, �@�@�|12�|y���|17��,y��5 �@�����, x���|4, y��5
�U ���̌������,
�@�`�Q�Ԗ��̈ꕔ �i���܂��j�` �P �E �@�A ���v��20���@�C ���[�h��2�� �@�G ���ϒl1.95����葽���̂�12�l �Q a�|3b��5 �R (�E���}�Q��) �\�ʐρ���ʐ�(�~)�~2�{���ʐ�(�����`) 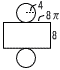 �@��42���~2�{8�~8�� �@��42���~2�{8�~8���@��32���{64����96�� (cm2) �S �^���������ƂȂ�̂�, �@b��1�̂Ƃ�,a��1,3,5 �@b��2�̂Ƃ�,a��3 �@b��3�̂Ƃ�,a��5 �@�@5�ʂ肾����, 5/36 |
16�x�R�� | �P 7�|16���|9
�R ��12�|��3��2��3�|��3����3 �S 6a�|9�|4a�{8��2a�|1
�@4��a/6���, a��24 �@��y��24/x��x���|3��������, �@y��24��(�|3)���|8 �U (x�|4)(x�|7)��0���,x��4,7 �V 3x��5(y�|4) �W (�E��̕\�Q��) �@�a��3,6,9,12�ɂȂ�̂�12�ʂ�
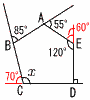 �X (�E�}�Q��) �@�O�p�̘a��360��������, �@��x�̊O�p �@�@��360�|(85�{55�{60�{90) �@�@��360�|290��70�� �@�����,��x��180�|70��110�� 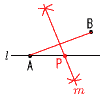 10 �E�} 10 �E�}�E2�_A,B������ �E����AB�̐������� �@�@�@m������ �El��m�̌�_�ɓ_P���Ƃ� |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| �m�g�b�v�ɖ߂��n�@�m�O�y�[�W�ɖ߂��n�@�m���y�|�W�ɐi���n |