| 1 |
(1) |
 -1-5 -1-5
|
6 |
空間内の平面について述べた文として適切でないものを,次のア~エの中から1つ選び,その記号を書きなさい。
ア
|
一直線上にある3点をふくむ平面は1つに決まる。 |
イ
|
交わる2直線をふくむ平面は1つに決まる。 |
ウ
|
平行な2直線をふくむ平面は1つに決まる。 |
エ
|
1つの直線とその直線上にない1点をふくむ平面は1つに決まる。 |
|
| (2) |
 (-3)2+4×(-2) (-3)2+4×(-2)
|
| (3) |
10xy2÷(-5y)×3x
|
| (4) |
|
| (5) |
(√5+3)(√5-2)
|
7 |
あるクラスの生徒14人の反復横とびの回数を測定したところ,全員が異なる回数であった。その測定した回数の少ない順に並べたとき,7番目の生徒と8番目の生徒の回数の差は6回で,中央値は48.0回であった。このとき,7番目の生徒の回数は何回か,求めなさい。
|
| 2 |
次の等式をrについて解きなさい。
l=2πr
|
| 3 |
次の方程式を解きなさい。
x2=9x
|
8 |
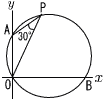
 下の図のように,座標平面上の原点Oを通る円がある。この円は,原点Oのほかに,y軸と点A(0,4)で,x軸と点Bで交わる。この円の原点Oをふくまない方の弧AB上に点Pをとると,∠OPA=30°であった。 下の図のように,座標平面上の原点Oを通る円がある。この円は,原点Oのほかに,y軸と点A(0,4)で,x軸と点Bで交わる。この円の原点Oをふくまない方の弧AB上に点Pをとると,∠OPA=30°であった。
このとき,この円の中心の座標を求めなさい。
|
| 4 |
yはxに比例し,x=-3のとき,y=18である。x=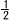 のときのyの値を求めなさい。 のときのyの値を求めなさい。
|
| 5 |
正n角形の1つの内角が140°であるとき,nの値を求めなさい。
|
