全国公立高校入試 　１番問題　【令和３年春】	正　答　１
	１　北海道　〜　８　茨城県

１北海道	１ (1) 3＋6＝9 　(2) 9×(−5)＋4＝−41 　(3) 2√7−√7＝√7 ２ イ 　ア y＝50x(比例) 　イ y＝ 300 (反比例) x 　ウ y＝x＋100(一次関数) 　エ y＝5πx2（二次関数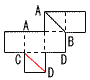） ３ 右下図 ４ 傾き3,切片2の直線で y＝3x＋2 ５ 下式を上式に代入して 　2x＋(3x＋1)＝11 　5x＝10より, x＝2 　これを下式に代入して, 　　y＝3×2＋1＝7で, y＝7 　よって, x＝2, y＝7 ６ 弧AB＝円周の長さ× 60 360 　＝18π× ＝3πcm	４岩手県	１ −6＋8＝2 ２ 4a−2b＋3a＋6b＝7a＋4b ３ 5＋3√5−4＝1＋3√5 ４ (x＋6)(x−6) ５ 解の公式より, 　x＝ −3±√32−4×1×1 ＝ −3±√5 2×1 2 　〜２・３番問題（おまけ）〜 ２ 両辺を入れ替えて,2πr＝Ｌ 　両辺を2πで割って, r＝ 　Ｌ . 2π ３ 反比例の式に,ある1点の座標を代入してみる 　たとえば, y＝ に(3,4)を代入すると, 　　4＝ a より,a＝4×3＝12 3 よって, y＝
２青森県	１ (1) −6 　 (2) 9−8＝1 　(3) 　10xy2×3x ＝−6x2y 　−5y 　(4) 　3(2x−y)−(5x＋y) ＝ x−4y 　3 3 　(5) 5＋√5−6＝−1＋√5 ２ 両辺を入れ替えて, 2πr＝l 　両辺を2πで割って, r＝ 　l . 2π ３ x2−9x＝0 　x(x−9)＝0より, x＝0,9 ４ y＝axに(−3,18)を代入して, 　18＝−3aで,比例定数a＝−6 　y＝−6xに,x＝を代入して 　　y＝−6×＝−3 ５ 1つの外角＝180−140＝40° 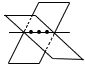　外角の和は360°だから 　　n＝360÷40＝9 ６ (右図参照) ア 　3点が,異なる2平面の交線上の場合がある ７ 14人の中央値は,7･8番目の平均値 　7番目をx回とすると, 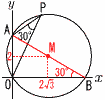　中央値＝ x＋(x＋6) ＝48.0 2 　　2x＋6＝96より, x＝45回 ８ (右図参照) 　∠AOB＝90°だから,ABは直径 　∠B＝∠P＝30° 　OA＝4より,OB＝4√3 　円の中心をMとすると, 　　MはABの中点で, (2√3,2)	５山形県	１ (1) 2−(−5)＝2＋5＝7 　(2) 　4−9 × 6 ＝ −5×6 ＝− 　12 5 12×5 　(3) 　16x2×9xy3 ＝12x2y 　12xy 　(4) 3√2− 　10√2 ＝3√2−5√2＝−2√2 √2√2 ２ 3x2＋2x−12x−8＝−8x−5 　移項して, 3x2−2x−3＝0 　解の公式より, 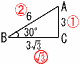　x＝ 1±√12−3×(−3) ＝ 1±√10 3 3 ３ (右図参照) 　底面の3辺は,1:2:√3で 　AC＝3,BC＝3√3だから, 　体積＝( ×3√3×3)×4＝ 18√3 cm3 ４ それぞれの確率を求める 　A (1,3)で,確率＝1/3 　B (4,6)で,確率＝1/3 　C (7,9) (8,10)で,確率＝2/6＝1/3 　　確率はすべて同じ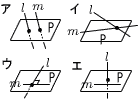で, エ ５ (右図参照)　エ 　ア 平行な場合もある 　イ 交わる場合もある 　ウ lとPが斜めに交わる場 　　合もある 　エ lとmは交わらないし,平行でもない
３秋田県	【前期】 １ (−9)×(−2)＝18 ２ a×(1＋0.1)＝1.1a円 ３ 　√24 ＝√8＝ 2√2 　√3 ４ 移項して, 2b＝1−3a 　両辺を2で割って, b＝ 1−3a 2 　　b＝ −3a＋1 も可 2 ５ 下式を上式に代入して, 　4x−3(−3x＋5)＋2＝0 　4x＋9x−15＋2＝0 　13x＝13より, x＝1 　これを下式に代入して, 　　y＝−3×1＋5＝−3＋5＝2 　よって, x＝1, y＝2 ６ x(x＋7)＝0より, x＝0,−7 ７ ウ 　〜２番問題（おまけ）〜 １ 変化の割合(傾き)＝ yの増加量 ＝3より, xの増加量 　yの増加量＝3×(xの増加量)＝3×3＝9 ２ (大,小)＝(1,4) (2,2) (4,1)の3通りだから 　確率＝3÷36＝ ３ 3数を2乗して比べる 　(√18)2＝18　　42＝16 　()2＝196/9≒21.8 　よって最大は, ４ 高さをhとすると, 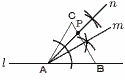　体積＝×52×h＝50 　h＝50×3÷25＝6cm ５ 右上図 　∠A(60°)を4分割すればよい ・∠Aの二等分線mをひく ・mの上側の角の二等分線nを引く ・nとBCの交点をPとする 【一般】 １ 4＋12＝16 ２ 　3(x−2y)−(3x−y) ＝− y 　6 ３ x2＋xy−12y2−xy＝x2−12y2 ４ 与式＝a(a＋2)＝(√3−1)(√3−1＋2) 　　＝(√3−1)(√3＋1)＝3−1＝2 ５ 　 x＝9より, x＝9× ＝6 ６ 追加の牛乳をxmLとすると, 　450:(180＋x)＝5:3 　5(180＋x)＝450×3 　5x＝1350−900 　5x＝450より, x＝90mL ７ 上式×2＋下式より, 　9y＝9で, y＝1 　これを上式に代入して, 　　x＋4＝−1で,x＝−5 　よって, x＝−5, y＝1 ８ 解の公式より, 　x＝ −(−5)±√(−5)2−4×2×1 2×2 　　＝ 5±√25−8 ＝ 5±√17 4 4 ９ ウ 　平均値＝(1＋4＋9＋16＋30＋18＋7)÷20 　　＝85÷20＝4.25 　中央値＝(4＋5)÷2＝4.5 　最頻値＝5 10 2乗して,100＜n＜121 　n＝7×○2の形だから, n＝7×42＝112 11∠x＝44＋62＝106° 12 面積＝52π× 240 ＝25π× 2 ＝ 50 π 360 3 3 cm2 13 △OABは正三角形で,∠AOB＝60° 　∠C＝30°で,∠BAC＝180−78−30＝72° 14 AB軸の円錐＝×32π×2＝6π 　　BC軸の円錐＝×22π×3＝4π 　よって, 6π÷4π＝倍 (1.5倍も可) 15 103＝1000より, 立方体の1辺は10cm 　三角錐H-DEG＝×(×102)×10＝500/3 　△DEGは1辺10√2の正三角形で, 　　△DEG＝×(10√2)2＝50√3 　高さをhとすると, 　三角錐H-DEG＝ 1 ×50√3×h＝ 500 3 3 　h＝ 　500 . ＝ 10 ＝ 10√3 　 50√3 √3 3 cm	６宮城県	１ −14＋5＝−9 ２ 　 ×(−4)＝−6 ３ 与式＝2ab2＝2×3×(−2)2＝6×4＝24 ４ 4a＝5b＋3c 　　a＝ 5b＋3c 　（a＝b＋cも可） 4 　 ５ 3√3＋ 　3√3 . ＝3√3＋√3＝4√3 √3√3 ６ (x＋5y)(x−5y) ７ イ,オ 　ア 0〜60分の階級に8人いる 　ウ 平均値＝(30×8＋90×13＋150×11 　　　　　　＋210×6＋270×2)÷40 　　　　　＝4860÷40＝121.5分 　エ 中央値は20・21番目で,60〜120分の階級 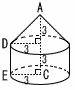８ (右図参照)　 　体積＝円錐＋円柱 　　＝×32π×3＋32π×3 　　＝9π＋27π＝36πcm3
		７福島県	１(1) −24 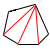　(2) 　3−5 ＝− 2 ＝− 1 6 6 3 　(3) 　(−8x3)×(−x) ＝2x2 　4x2 　(4) 5√2＋√2＝6√2 ２ (右図参照) 　六角形は,三角形4つに分割できるから, 　内角の和＝360×4＝720° 　〜２番問題（おまけ）〜 １ −3＜−2√2 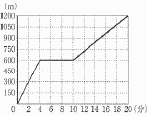　両辺を2乗すると,9＞8 　共に負だから, 　不等号の向きは逆になる ２ 126×＝36 (人) ３右図 ４ 変化の割合＝ 62a−22a ＝ 32a ＝−4 6−2 4 　32a＝−16より, a＝− ５ エ
		８茨城県	１ 3−7＝−4 ２ 2(√10−√5)＋2√5＝2√10 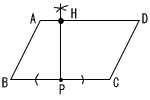３ ウ ４ 右図 　・PからBCの垂線をひく 　・垂線とADの交点を 　　　Hとする 　〜２番問題（おまけ）〜 １ ア n＋1　イ n＋2　ウ n＋1 ２ ア x(x＋5)　イ −8　ウ 3 ３ ア 2　イ 8 　Aのx座標は1で, 　　これをy＝に代入して,A(1,2) 　Aの座標をy＝ax2に代入して,a＝2 　変化の割合＝ 2×32−2×12 ＝ 18−2 ＝8 3−1 2 ４ 次のいずれか ・Aさんの場合 　　最頻値は,Aが11.9秒,Bが12.0秒で, 　　Aが小さいから早く走れそう。 ・Bさんの場合 　　中央値は,Bが12.0秒,Aが12.1秒で, 　　Bが小さいから早く走れそう。