全国公立高校入試 　１番問題　【令和２年春】

（３１）鳥取県

学習日　　　 月　　 　日（　　　）

〜 印刷して、紙の上でやってネ！ （文字サイズを小にするとＡ４に収まります）〜

1	(1)  2−(−5)	７	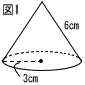右の図１のように,底面の半径が3cm,母線の長さが6cmである円錐の側面積を求めなさい。
	(2) ()÷(−)
	(3) 6√3−√27−√12	８	ある養殖池にいるニジマスの総数を調べるために,次の実験をした。 　網ですくうと50匹とれ,その全部に印をつけて池にもどした。数日後,再び同じ網ですくうと48匹とれ,印のついたニジマスが6匹いた。 　この池にいるニジマスの総数を推測しなさい。
	(4) 3(2x−y)−2(x＋y)
	(5) 3a2b×4ab2÷2ab	９	図2において,3点A,B,Cを通る円の中心Oを作図しなさい。 　ただし,作図に用いた線は明確にして,消さずに残しておき,作図した円の中心Oには記号Oを書き入れなさい。
２	(2a−3)2
３	a＝−2のとき,−a2−2a−1の値を求めなさい。
４	x2−3x−10 を因数分解しなさい。
５	次の表は,yがxに反比例する関係を表したものである。yをxの式で表しなさい。また,表のアにあてはまる数を答えなさい。 x … -1 0 1 2 … y … -12 × 12 ア …
６	二次方程式 x2−3x−1＝0 を解きなさい。

印刷時に改ページ

10	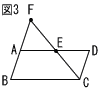右の図3のように,平行四辺形ABCDがある。点Eは辺ADの中点とし,直線BAと直線CEの交点をFとする。 　このとき,△AEF≡△DECであることを次のように証明した。 　□に証明の続きを書き,証明を完成しなさい。　 （証明）△AEFと△DECで、	11	ある中学校では,次のルールで行われる的当て大会が開催される。 　[ルール] ・ 　 右の図4のような的に向かって,ボールを１人が３回ずつ投げる。 ・ 　 ボールが的に当たった場合,当たった場所の数を得点とする。 ・ 　 ボールが的に当たらなかった場合,得点は0点とする。 ・ 　 ３回のうちの最高得点を競い,最も高い得点てあった人の勝ちとする。 　3年1組では,クラス代表を決めるため,1人が10回ずつ的に向かってボールを投げ,その得点を計測した。その結果,そらさんとあずまさんのどちらかを選ぶことになった。2人の得点分布は次の図5,図6のとおりであった。 　あずまさんを代表として選ぶとき,その理由を平均値,中央値,最頻値のいずれかを根拠として使い,説明しなさい。 　図5　そらさんの得点分布（平均値5.9点） 図6　あずまさんの得点分布（平均値5.9点）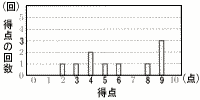
	△AEF≡△DEC　　（証明終）