|
正 答 ４ | |||
| 25 滋賀県 〜 32 島根県 |
|
正 答 ４ | |||
| 25 滋賀県 〜 32 島根県 |
〜 印刷して、紙の上でやってネ！ （文字サイズを小にするとＡ４に収まります）〜
| 25滋賀県 | １ (−11)＋(＋6)＝−5人
3×2＋2y＝8で,y＝1 よって,x＝2,y＝1 ４ 2√3−3√2 ５ (x−3)(x−4)＝0より,x＝3､4
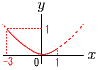 ７(右図参照)y＝ax2に(−3,1)を代入 1＝9aで,a＝  ８ 最多は28人で,7点 ９ △DFCと等積なのは, △AFC,△AFD､△ACDの3通り カードの引き方は全部で, 4×3÷2＝6通り よって,確率＝3÷6＝  |
28兵庫県 | １ −2 ２ 2x＋3y ３ 2√2＋3√2＝5√2 ４ 上式×2＋下式より, 7x＝21で,x＝3 これを上式に代入して, 3×3＋y＝4で,y＝4−9＝−5 よって,x＝3,y＝−5 ５ 解の公式より,
６ y＝  に(2,−8)を代入すると,−8＝a/2で,a＝−16 y＝−16/xにx＝4を代入して, y＝−16/4＝−4 ７ (  )2＝ ８ △BCDで, BDは半径だから,∠BCD＝90° ∠D＝∠A＝42°(円周角) ∠x＝180−(90＋42)＝48° |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 26京都府 | 【 前期 】 １ 8×  ＋16＝18＋16＝34
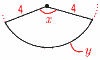 ４(右図参照)弧の長さをyとすると, 面積より, ×y×4＝6π2y＝6πで,y＝3π y＝8π×  より、x＝3π÷8π×360＝135° ５ 元の式に(5,−3)を代入すると,
これを上式に代入して, 5×7＋3b＝23で,b＝−4 よって,a＝7,b＝−4 ６ 与式＝(a＋5)(a＋7) ＝(√30−6＋5)(√30−6＋7) ＝(√30−1)(√30＋1)＝30−1＝29 ７ 解の公式より,
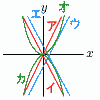 ８(右図参照) ア,ウ,カ ９ 6個から2個取り出すのは, 6×5÷2＝15通り 黒が少なくとも1個残る確率 ＝1−(黒玉が残らない確率) ＝1−(2個とも黒玉を取り出す確率) ＝1−  ＝ |
29奈良県 | 【 一般 】 １ (1) −3 (2) −4×9＝−36 (3) 2a2＋3b (4) x2＋2xy＋y2−5xy＝x2−3xy＋y2 ２ 0,±1,±2,±3で, 7個 ３ 解の公式より,
 y＝12/xにx＝−2を代入して,Aの値は,y＝12÷(−2)＝−6 ５(右図参照) 底面の円周＝おうぎ形の弧＝10π 24π× ＝10πより,∠x＝１０π÷24π×360＝150° ６ ア,エ ア 5÷31≒0.16 〇 イ 26.0−24.0＝2.0 × ウ 5＋7＋5＋5＝22日 × エ 8日で、(28.0−26.0)÷2＝27.0℃ 〇 オ (32.0−30.0)÷2＝31.0° × ７ (1) 5個から2個を取り出す方法は全部で, 5×4÷2＝10通り
８ (1) B＝10y＋x
 2y−y＝y＝4で,x＝8よって,A＝84 【 特色 】
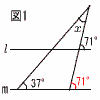
２ (x＋4)(x−3)＝0より, x＝−4,3 ３(右上図参照) ∠x＝71−37＝34° ４ ウ ５ 右表より19通りだから, 確率＝19/36 ６ 順に並べると, 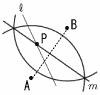 37,41,43,46,50,57,62,64で,（46＋50)÷2＝48回 ７ 体積＝  π×33÷2＝18πcm3８ 右図 ・線分ABの垂直二等分線mを引く ・l とmの交点をPとする |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 【 中期 】 １ 5−36＝−31 ２ 12x＋4y−5x＋8y＝7x＋12y ３ √3×4√2＋3√6＝4√6＋3√6＝7√6 ４ 上式×3−下式×2より, 15y−14y＝−21＋18で,y＝−3 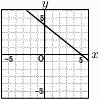 これを上式に代入して,2x−15＝−7で,x＝4 よって,x＝4,y＝−3 ５ 右図 切片が4で, 傾きが−  の直線６ 各辺を2乗すると、 25＜n＜36だから, n＝26,27,・・・,35で,10個 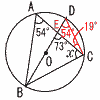 ７(右図参照)∠D＝∠A＝54° △CDEで, ∠DCE＝73−54＝19° ∠BCD＝90°だから, ∠x＝90−19＝71° ８ 不良品をx個とすると,
およそ230個 |
30和歌山県 | １ (1) −3 (2) 1− ＝ (3) 2a＋8b＋3a−6b＝5a＋2b
(5) (x2＋2x＋1)＋(x2−2x−8) ＝2x2−7 ２ (3x)2−(2y)2＝(3x＋2y)(3x−2y) ３ √10−n＞0より,10−n＞0 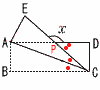 つまり,0＜n＜10で考える条件に合うのは, n＝1,6,9 ４(右図参照) ∠ACE＝∠ACB＝20° ∠CPD＝∠ECB＝40° ∠x＝180−40＝140° ５ 条件に合うのは,次の6通り (和夫,花子)＝(1,4〜6) (2,5〜6) (3,6) さいころの目の出方は全部で,6×6＝36通り よって,確率＝6/36＝  |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 27大阪府 | 【 A 】 １ −17 ２ −  ３ 3×4＝12 ４ x＋4＋5x−15＝6x−11 ５ 2xy2 ６ 3√5＋5√5＝8√5 〜２番問題（おまけ）〜 １ 2×(−8)＋7＝8−16＋7＝−9 ２ 4.6−(−1.3)＝4.6＋1.3＝5.9℃ ３ エ ア y＝6x＋30 (1次関数) イ y＝500/x (反比例) ウ y＝140−x (1次関数) エ y＝25x (比例) ４ 上式＋下式より、 6x＝18で,x＝3 これを上式に代入して, 5×3＋y＝22で,y＝22−15＝7 よって,x＝3,y＝7 |
31鳥取県 | １ (1) 2＋5＝7 (2) ×(− )＝−5(3) 6√3−3√3−2√3＝√3 (4) 6x−3y−2x−2y＝4x−5y
３ 与式＝−(a＋1)2＝−(−2＋1)2＝−1 ４ (x−5)(x＋2) ５ y＝  に(1,12)を代すると,a＝12式は,y＝  x＝2のときアは,y＝12/2＝6 ６ 解の公式より,
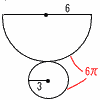 ７(右図参照)扇形(側面)の弧＝底面の円周 ＝6πcmだから, 側面積＝ ×6π×6＝18πcm2８ 総数をx匹とすると,
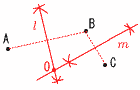 ９ 右図・線分ABの 垂直二等分線l を引く ・線分BCの 垂直二等分線mを引く ・l とmの交点をOとする 10 AE＝DE(EはADの中点) ∠AEF＝∠DEC(対頂角) ∠EAF＝∠EDC(平行線上の錯角) 1組の辺とその両端角が等しいから 11最頻値を比較すると,そらさんの 7点より,あずまさんの9点が大きいから |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 【 B 】 １ −3＋25＝22
５ エ,オ アは逆, イは不定, ウは正 ６ √189n＝3√21nより, n＝21 ７ 20×3.6＋12×4.0＋8x＝3.5×40 8x＝140−72−48より, x＝2.5冊 ８ 8の倍数になるのは, 16,24,32,56,64の5通りだから, 5/36 ９ C(7,−6)より,A(〇,−6)､B(7､〇) y＝−  x2にy＝−6を代入すると,−6＝− x2で,x2＝16よって,A(−4,−6) 直線AOの傾きは,(−6)÷(−4)＝  …アy＝ax2にx＝7を代入すると, y＝49aで,B(7,49a) 直線OBの傾きは,49a÷7＝7a…イ ア＝イより, ＝7aで, a＝3/14 |
32島根県 | １ 5＋6＝11
４ みかん5個とりんご3個の合計金額は 1000円以下である。 ５ (a＋10)(a−2) ６ 解の公式より,
y＝−12/xにx＝−2を代入して, 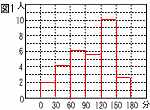 y＝−12÷(−2)＝6８ ●＝30−(2＋4＋5 ＋10＋3)＝6 (1) 最多は10で, (150-120)÷2＝135分 (2) 右図 ９(右図参照) 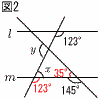 (1) ∠x＝180−123＝57°(2) ∠y＝57＋35＝92° 10 (1) AC＝√22＋22＝√8 ＝2√2cm (2) (下図参照) 体積は円錐2個分 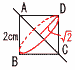 円錐の高さは√2cmで,直径はBD＝AC＝2√2cm 半径は2√2÷2＝√2cm 体積＝  ×(√2)2π×√2×2＝ √2πcm3 |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ［トップに戻る］ ［前ページに戻る］ ［次ペ−ジに進む］ |
