|
(26)京都府 | 学習日 月 日( ) |
|
(26)京都府 | 学習日 月 日( ) |
| 【 前 期 】 | |||||||
| 1 | 7 | 二次方程式 3x2−8x−4=0 を解け。 |
|||||
| 2 |
|
||||||
| 3 | |
8 | x<0の範囲で,xの値が増加すると対応するyの値も増加する関数を,次のア〜力からすべて選べ。 ア y=2x イ y=−2x ウ y=2x−1 エ y=−2x+1 オ y=2x2 カ y=−2x2 |
||||
| 4 | 半径4cm,面積6πcm2のおうぎ形の中心角の大きさを求めよ。 |
||||||
| 5 |
|
9 | |||||
| 6 | a=√30−6のとき,a2+12a+35の値を求めよ。 |
||||||
| 【 中 期 】 | ||||||
| 1 | 6 | 5<√n<6 をみたす自然数nの値を求めよ。 |
||||
| 2 | 4(3x+y)−6( |
|||||
| 3 | √3×√32+3√6 |
7 | 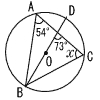 次の図で,4点A,B,C,Dは円Oの周上にあり,線分BDは円Oの直径である。このとき,∠xの大きさを求めよ。 次の図で,4点A,B,C,Dは円Oの周上にあり,線分BDは円Oの直径である。このとき,∠xの大きさを求めよ。 |
|||
| 4 | 次の連立方程式を解け。
|
8 | ある工場で同じ製品を10000個作った。このうち300個の製品を無作為に抽出して検査すると,7個の不良品が見つかった。この結果から,10000個の製品の中に含まれる不良品の個数はおよそ何個と考えられるか。一の位を四捨五入して答えよ。 |
|||
| 5 | 一次関数 y=−x+4 のグラフをかけ。 |
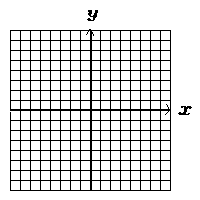 |
||||
| [トップに戻る] [前ページに戻る] [次ペ−ジに進む] [答のペ−ジに進む] |