全国公立高校入試 　１番問題　【平成３１年春】

（４２）長崎県

学習日　　　 月　　 　日（　　　）

〜 印刷して、紙の上でやってネ！ （文字サイズを小にするとＡ４に収まります）〜

【　Ａ問題　】
1	8＋(−2)×3	７	x2＋6x＋8 を因数分解せよ。
２	−	８	2次方程式 x2＋5x＋2＝0 を解け。
３	√12−4√3
４	x＝5,y＝−1のとき,3(x＋y)−(2x−y)の値を求めよ。	９	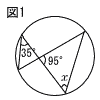図1のような円において,∠xの大きさを求めよ。
５	次の(1)〜(4)のうち,yがxに反比例するものを１つ選び,その記号を書け。 (1) 　  100Ｌの水をxＬ使ったときの残りの水の量yＬ (2)  半径xcmの円の面積ycm2 (3) 　  時速4kmでx時間歩いたときの進んだ道のりykm (4) 　  面積6cm2の三角形の底辺の長さxcm,高さycm	10	図2において,∠AOBの二等分線を定規とコンパスを用いて解答用祇の図2に作図せよ。ただし,作図に用いた線は消さずに残しておくこと。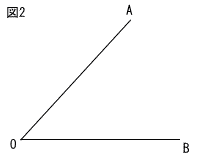
６	連立方程式 { 3x−y＝4  を解け。  x−2y＝3

印刷時に改ページ

【　Ｂ問題　】
1	(√2−√6)2＋ 　12 . √3	６	次の(1)〜(5)のうち,yがxに反比例するものを１つ選び,その記号を書け。 (1) 　  100Ｌの水をxＬ使ったときの残りの水の量yＬ (2)  半径xcmの円の面積ycm2 (3) 　  時速4kmでx時間歩いたときの進んだ道のりykm (4) 　  面積6cm2の三角形の底辺の長さxcm,高さycm (5)  1辺の長さxcmの正三角形の周の長さycm
２	12a2b3÷ ab2×(−2b)2
３	等式 Ｓ＝(a＋b)h をaについて解け。	７	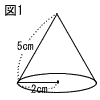図1の円錐の展開図をかくとき,側面になるおうぎ形の中心角の大きさを求めよ。
４	2次方程式 (x＋1)(x＋4)＝2(5x＋1) を解け。	８	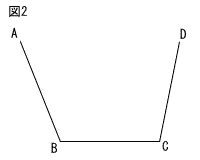図2において,3つの線分AB,BC,CDのすべてに接する円の中心Pを定規とコンパスを用いて解答用紙の図2に作図して求め,その位置を点・で示せ。ただし,作図に用いた線は消さずに残しておくこと。
５	√67−2n の値が整数になるような自然数nのうち,最も小さいものを求めよ。