全国公立高校入試 　１番問題　【平成３1年春】	正　答　６
	41　佐賀県　〜　47　沖縄県

〜 印刷して、紙の上でやってネ！ （文字サイズを小にするとＡ４に収まります）〜

41佐賀県	１ (1) 3　　(2) − 　(3) 5√3−4√3＝√3 　(4) 　3(x＋y)−2(x−y) ＝ x＋5y  　2×3 6  ２ (x−8)(x＋7) ３ 6a＋5b≦1000 ４ y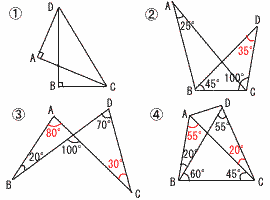＝に(2,4)を代入して, 　4＝ a 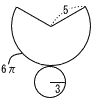より,a＝8で, y＝  8 2 x ５ 解の公式より, x＝ −(−7)±√(−7)2−4×1×2 ＝ 7±√41 2×1 2 ６(右図参照) �@と�C ７(右図参照) 円錐 側面積(扇形) 　＝×6π×5＝15π 底面積(円) 　＝32π＝9π よって,15π＋9π＝24πcm2 　〜追加問題〜 １ √82−12＝√63＝3√7 ２ y座標が0,1,2,…,7の 8個 ３ 58個　　４ 38個	44熊本県	１ ２ 7＋6＝13 ３ 7x＋y−5x＋8y＝2x＋9y ４  　　48a2b2　. ＝−3a  −4a×4b2 ５ 9x2−6x＋1＋6x−6x2＝3x2＋1 ６ 3√10＋ 　60√10 . √10√10 　＝3√10＋6√10＝9√10 　〜２番問題（おまけ）〜 1 両辺を5倍して,2x＋9＝5ｘ 　−3x＝−9より,x＝3 ２ (1) (2019−9)×＝2010×＝1340 (2) y＝(x−9) …ア 　　(y−9)＝2 …イ 　イより,y−9＝2÷＝2×＝3 　　y＝3＋9＝12 …ウ 　ウをアに代入して,12＝(x−9) 　　x−9＝12÷＝12×＝18 　　x＝18＋9＝27 よって,x＝27,y＝12
42長崎県	【　Ａ　】 １ 8−6＝2 ２ 　9−4 ＝  12 ３ 2√3−4√3＝−2√3 ４ 与式＝3x＋3y−2x＋y＝x＋4y 　＝5＋4×(−1)＝5−4＝1 ５ (1) y＝100−xで,1次関数 　(2) y＝πx2で,2乗に比例 　(3) y＝4xで,比例 　(4) 　 xy＝6より,y＝ で,反比例 よって反比例は,(4) ６ 上式×2-下式より,5x＝5で,x＝1 　これを上式に代入して,3−y＝4で,y＝−1 よって,x＝1,y＝−1 ７ (x＋2)(x＋4) ８ 解の公式より, 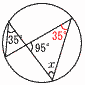x＝ −5±√52−4×1×2 ＝ −5±√17 2×1 2 ９(右図参照) 　∠x＝180−(95＋35)＝50° 10 下図 ・Oから,OC＝ODとなる点をとる ・CとDから,CP＝DPとなる点Pをとる	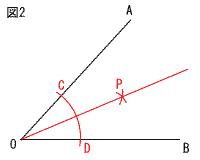45宮崎県	１ −7＋5＝−2 ２ 　−18＋25 ＝  7  　30 30 ３ 16＋14＝30 ４ −3a＋3b＋4a−5b＝a−2b ５ 3√2−4√2＋6√2＝5√2 ６ 移項して,x2−x＝0 　x(x−1)＝0より,x＝0,1 ７ 10人の合計＝平均値×10だから, Eをx冊とすると, 　(3+4+…+x+…+4)＝3.6×10 　x＋32＝36より,x＝4 ８ ウ
	【　B　】 １ 2−2√12＋6＋ 　12√3 8−4√3＋4√3＝8 √3√3 ２ 　12a2b3×3×4b2 ＝36ab3  　4ab2 ３ 両辺を入れかえて, (a＋b)h＝S 　両辺×2で,(a＋b)h＝2S 　両辺÷hで,a＋b＝ 2S h 　移項して,a＝ 2S −b h ４ x2＋5x＋4＝10x＋2 　x2−5x＋2＝0 解の公式より, 　x＝ −(−5)±√(−5)2−4×1×2 ＝ 5±√17 2×1 2 ５ 与式＝kとすると,k2＝67−2n 　nは自然数だから,1≦k2≦65 k＝8のとき,2n＝67−82＝3(不適) k＝7のとき,2n＝67−72＝18より,n＝9(適) ６ (1) y＝100−xで,1次関数 　(2) y＝πx2で,2乗に比例 　(3) y＝4xで,比例 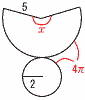　(4) 　 xy＝6より,y＝ で,反比例 　(5) y＝3xで,比例 よって反比例は,(4) ７(右図参照) 扇形の弧＝10π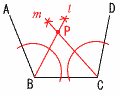×…ア 円周＝4π…イ ア＝イより,  x π＝4πで, 36 　x＝36×4＝144° ８ 右図 ・∠Bの2等分線l を引く ・∠Cの2等分線mを引く ・l とmの交点をPとする	46鹿児島県	１ (1) 5×4−20 　(2) 　1 ＋ 5×9 ＝ ＋ ＝ 　4 3×10 　(3) 2√7−2√5＋√5−√7＝√7−√5 　(4) 2は含まないから白丸で,ウ 　(5) x＝4を代入して成り立つのは, ア エ 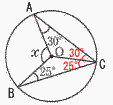２(右図参照) △OAC,△OBCはともに 　二等辺三角形だから, ∠x＝(30＋25)×2＝110° ３ x＝3のとき,y＝32＝9 　x＝6のとき,y＝62＝36 よって,変化の割合＝ 36−9 ＝9 6−3 ４ 高さは等しいから,底面積に比例, 　つまり(相似比)2に比例で,22＝4倍 ５ 鹿児島県の収穫量割合をxとすると, 　1733:5153＝14.2:x 　1733x＝5153×14.2 よって,x＝ 5153 ×14.2で，イ 1733
43大分県	１ (1) −7　　(2) −9＋8＝−1 　(3) 6a＋b−3a＋5b＝3a＋6b 　(4) 　2(2x＋y)＋(5x−7y) ＝ 9x−5y  　6 6 　(5) 6＋2√18＋3＝9＋6√2 ２ 移項して,x2−3x−2＝0 解の公式より, x＝ −(−3)±√(−3)2−4×1×(−2) ＝ 3±√17 2×1 2 ３ 129.5≦a＜130.5 ４ 　x ＋ 1200−x ＝ x＋1200 　(分) 　60 120 120 ５ 和が3の倍数となる取り出し方は,次の9通り 　(1,3) (3,1) (1,5) (5,1) (2,4) (4,2) (3,3) 　 (4,5) (5,4) 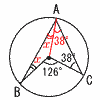よって,確率＝  9 ＝  9 5×5 25 ６(右図参照) ∠BAC＝126÷2＝63° ∠ABO＝∠BAO 　＝63−38＝25° 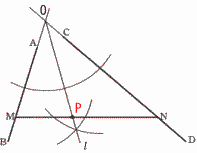７ 右図 ・BAとDCを延長し, 　交点をOとする ・∠BODの2等分線l 　を作図する ・MNとl の交点を 　Pとする	47沖縄県	１ −12 ２ − ３ 0.95 ４ 2√12＝4√3 ５ 25a2 ６ 2x＋2−1＋x＝3x−1 　〜２番問題（おまけ）〜 １ 6x＋4＝−8 　6x＝−12より,x＝−2 ２ 下式を上式に代入して, 　5x−3(2x−5)＝9 　5x−6x＋15＝9 　−x＝−6より,x＝6 　これを下式に代入して,y＝2×6−5＝7 よって,x＝6,y＝7 ３ x2＋8x＋16 ４ (x−3)(x−5) ５ �Bを因数分解すると,x(−3)＝0だから, 　正しくない変形は,�Bから�C ６ √36＜√45＜√49より,6＜√45＜7 ここで,√45は6.5より大か小か調べる 　6.52＝42.25だから,6.5＜√45＜7 中央の6.5より大きいから, 7

［トップに戻る］　［前ページに戻る］