全国公立高校入試 　１番問題　【平成３１年春】

（３１）鳥取県

学習日　　　 月　　 　日（　　　）

～ 印刷して、紙の上でやってネ！ （文字サイズを小にするとＡ４に収まります）～

１	(1) －7＋3－4	８	奇数を2乗して19をたすと4の倍数になる。このことを,次のように文字式を使って証明した。□に証明の続きを書き,証明を完成しなさい。 （証明）nを整数とすると,奇数は2n＋1と表される。この奇数を2乗して19をたすと, よって,奇数を2乗して19をたすと4の倍数になる。 　（証明終）
	(2) ÷(－)
	(3)　 　3 . ＋4√3－√27 √3
	(4) 4(2x－1)－3(2x－3)	９	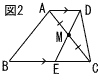図2のように,AD//BCである台形ABCDがある。線分ACの中点をMとし,直線DMと辺BCとの交点をEとする。 　このとき,AD＝CEであることを,次のように証明した。□に証明の続きを書き,証明を完成しなさい。 （証明）△AMDと△CMEで, △AMD＝△CME 合同な図形では,対応する辺の長さは等しいので, 　AD＝CE　　（証明終）
	(5) (－xy)2×10xy2÷5x2
２	(3x－1)(4x＋3)
３	a＝－3のとき,a2－2aの値を求めなさい。
４	x2－4x＋3 を因数分解しなさい。	10	図3のように,直線上に2点０,Ａがあり,０Ａ＝１とする。このとき,OP＝√2となる点Pを解答用紙の直線上に,以下の指示に従って作図しなさい。 　指示 ・点Ｐは点０よりも右側にとりなさい。 ・作図に用いた線は明確にして,消さずに残して 　　おきなさい。 ・作図した点Ｐには記号Ｐを書き入れなさい。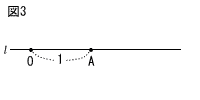
５	等式 V＝πr2h を,hについて解きなさい。
６	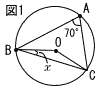図1において,3点,A,B,Cは点Oを中心とする円の周上の点である。このとき,∠xの大きさを求めなさい。
７	二次方程式 5x2＋3x－1＝0 を解きなさい。