|
正 答 4 | |||
| 25 滋賀県 〜 32 島根県 |
|
正 答 4 | |||
| 25 滋賀県 〜 32 島根県 |
〜 印刷して、紙の上でやってネ! (文字サイズを小にするとA4に収まります)〜
| 25滋賀県 | 1 15−19=−4℃
これを上式に代入して,x+4=7で,x=3 よって,x=3,y=−2
(x+5)(x−1)=より,x=−5,1
x2=4より,x=±2 8 1回出る確率は,青が3/6= (a) 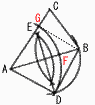 (b) (b) (c) 9 右図 FG//ABより, △AFG∽△ABD 面積比が1:2だから,相似比は1:√2 つまり,ABが対角線となるような正方形ADBE を作図し,その1辺ADの長さをABとAC上に とる。 交点をF,G(Eと重なる)とする。 |
28兵庫県 | 1 −7 2 2y 3 5√3−3√3=2√3 4 (x−4)(x+1)=0より,x=4,−1 5 −3=a/2より,a=(−3)×2=−6 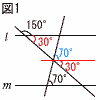 6(右図参照) 6(右図参照)∠x=70+30=100° 7 底面の半径をrとすると, 22+r2=32より, r=√9−4=√5 体積= 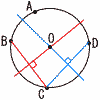 8(右図参照) ウ 8(右図参照) ウ |
|||||||||||||||||||||||||
| 26京都府 | 【 前期 】 1 (5+4)×(16/9)=16
与式=X2−2Xー24=(X−6)(X+4) =(76−6)(76+4)=70×80=5600 5 解の公式より,
A:B=x2:42=9:1で, x2=42×9=42×32=122で,x=12cm 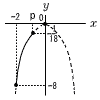 7(右図参照) 7(右図参照)最小値はy=−8だから, −8=−2x2より,x=−2 最大値はy=− − 8 3.05≦a<3.15だから, A ア B ク 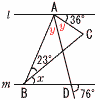 9(右図参照)
9(右図参照)∠y=76−36=40° (x+23)+(40×2+36)=180 ∠x=180−23−116=41° |
29奈良県 | 1 (1) −12 (2) 2×(−25)=−50
2 下式を上式に代入して, 2x−5(x−5)=−2 −3x=−27で,x=9 これを下式に代入して,y=9−5=4 よって,x=9,y=4 3 (x−9)(x+2)=0より,x=9,−2 4 2乗して比べる (3.3)2=1.89 ( (√11)2=11より, 最大は 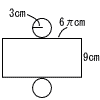 5(右図参照) 5(右図参照)側面(長方形)の横は,6πcm 表面積=底面積×2+側面積 =32π×2+9×6π =72πcm2 6 ∠BOC(大きい方の中心角) =116×2=232° よって,∠x=360−232=128° 7 2人を選ぶ方法は ア 4人から2人で,4×3÷2=6通り イ 各1人ずつで,4×2=8通り ウ 2人から2人で,1通り 全部の6人から2人は,6×5÷2=15 よって最大はイで,確率=8/15 8 (1) あ 20 い 3000−2250=750 (2) 追いついたのは,,10後で,2500mの地点 2500÷10=250m/分 |
|||||||||||||||||||||||||
| 【 中期 】 1 36−8=28
4 上式を下式に代入して, 9(2+y)−5y=2で,y=−4 これを上式に代入して,x=2−4=−2 よって,x=−2,y=−4 5 与式=3(a2−8a+16)=3(a−4)2 6 傾きが− y= 7 ∠AOB=75×2=150° 弧の長さは中心角に比例するから, x:360=4π:150で, x=4π×360÷150= 8 (少なくとも1枚は表の確率)は, 1−(3枚とも裏の確率)だから,
|
30和歌山県 | 1 (1) −3 (2) 4− (3) 6x−3y+8x−4y=14x−7y (4) 4√2−3√2+√2=2√2 (5) a2+a−3−a2+4a−4=5a−7 2 x(x−9)=0より,x=0,9 3 2x+2y=2より,y=−x+1 式が一次関数の形で, ウ 4 条件に合うのは,以下の14通り (a,b)=(1,1) (2,1) (2,2) (3,1) (3,3) (4,1) (4,2) (4,4) (5,1) (5,5) (6,1) (6,2) (6,3) (6,6) よって,確率=14/36=7/18 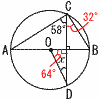 5(右図参照) 5(右図参照)円周角∠BCD=90−58=32° 中心角∠BOD=32×2=64° よって, ∠x=180−64−90=26° |
||||||||||||||||||||||||||
| 27大阪府 | 【 A 】 1 2+5=7 2 −12 3 13−16=−3 4 3x+7+3x−6=6x+1 5 8x3 6 5√2−3√2=2√2 〜2番問題(おまけ)〜 1 6×2−4=8 2 イ 3 3x=30より,x=10 4 最多は4人で,最頻値=55cm 【 B 】 1 16−(−3)=19 2 10a−6b−7a+14b=3a+8b
4 7−20=−13 5 最多は13個で,100〜110gの階級 (110+120)÷2=115g 6 イ (ア 正 ウ 正 エ 正または0) 7 (x+4)(x+5)=210で,x2+9x−190=0 (x+19)(x−10)=0より,x>0だから,x=10 8 3の倍数は,A6 B3 B6 の場合で, A6は,B1 B3 B5 の3通り B3は,A2 の1通り B6は,A2 A4 A6 の3通り
9 AとBの座標を求める y=x2にx=2を代入して,A(2,4) y= l をy=ax+bとして,A,Bの座標を代入すると,
|
31鳥取県 | 1 (1) −8 (2) (3) √3+4√3−3√3=2√3 (4) 8x−4−6x+9=2x+5
3 (−3)×(−3−2)=(−3)×(−5)=15 4 (x−1)(x−3) 5 両辺を入れかえて,πr2h=V
中心角∠BOC=70×2−140° 底角∠x=(180−140)÷2=20° 7 (2n+1)2+19=4n2+4n+20 =4(n2+n+5) nは整数だから,n2+n+5も整数で, 4×整数の形になるから,4の倍数 8 AM=CM (仮定) ∠MAD=∠MCE (錯角) ∠AMD=∠CME (対頂角) 1辺とその両端の角がそれぞれ等しいから, 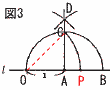 9 右図 9 右図・OA=ABとなる点Bをとる ・OBの垂線ADを引く ・OA=OCとなる点Cをとる ・OC=OPとなる点Pをとる |
|||||||||||||||||||||||||
| 32島根県 | 1 −9−2=−11 2 3 2×32×5 4 (2√2+1)(√2−3)=4−5√2−3=1−5√2 5 直線CD 6 ア 180°×(n−2) イ 360 7 条件式を計算して,整理すると,
1年生は 9 10 11 15 16 18 20 2年生は 10 12 13 14 x 17 20 22 中央値(赤字)が等しいから,
|
| [トップに戻る] [前ページに戻る] [次ペ−ジに進む] |