全国公立高校入試 　１番問題　【平成３１年春】

（２６）京都府

学習日　　　 月　　 　日（　　　）

〜 印刷して、紙の上でやってネ！ （文字サイズを小にするとＡ４に収まります）〜

【　前　　期　】
1	{5−(−22)}÷()2	７	関数y＝−2x2において,xの変域が−2≦x≦pのときのyの変域が−8≦y≦−(1/18)である。このときのpの値を求めよ。
２	7x−1 −x＋2   5
３	(3−√5)2＋ 　10 . √5	８	ある物体の重さを測定すると,3.1gであった。この数値は,小数第2位を四捨五入して得られた値である。この重さの真の値をagとし,aの範囲を次のような不等式で表すとき,[ A ]に当てはまる不等号を下のi 群(ｱ)･(ｲ)から, [ X ]に当てはまる数をii 群(ｶ)〜(ｹ)から,それぞれ1つずつ選べ。 　3.05≦a [ A ] [ X ]　 i 群 　(ｱ) ＜　(ｲ) ≦  ii 群 　 　(ｶ) 3.1　(ｷ) 3.14　(ｸ) 3.15 　（ｹ) 3.2
４	a＝30,b＝−23のとき, (a−2b)2−2(a−2b)−24 の値を求めよ。
５	二次方程式 3x2−3x−2＝0 を解け。	９	次の図で,2直線 l,mは平行であり,点Dは∠BACの二等分線と直線mとの交点である。このとき,∠xの大きさを求めよ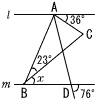
６	球Aの表面積が球Bの表面積の9倍であり,球Bの半径が4cmであるとき,球Aの半径を求めよ。

印刷時に改ページ

【　中　　期　】
1	(−6)2−42÷2	６	直線y＝−x＋5に平行で,点(−6,2)を通る直線の式を求めよ。
２	3a＋1 − 4a−7 　4 6
３	√27＋√24×√8	７	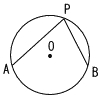右の図のように,円Oの周上に3点A,B,Pがあり,∠APB＝75°である。円周角∠APBに対する弧ABの長さが4πcmであるとき,円Oの周の長さを求めよ。
４	次の連立方程式を解け。 　{ x＝2＋y 9x−5y＝2
５	3a2−24a＋48 を因数分解せよ。	８	3枚の硬貸を同時に投げるとき,少なくとも1枚は表が出る確率を求めよ。ただし,それぞれの硬貨の表裏の出方は,同様に確からしいものとする