全国公立高校入試 　１番問題　【平成３１年春】

（６）宮城県

学習日　　　 月　　 　日（　　　）

〜 印刷して、紙の上でやってネ！ （文字サイズを小にするとＡ４に収まります）〜

【　前　　期　】
1	4＋7×(−2)	７	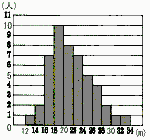ある中学校で3年生男子48人のハンドボール投げの記録をとりました。右の図は,今回の記録を,階級の幅を2mとして整理し,ヒストグラムに表したものです。 　今回の記録の平均値は22.1mでした。今回の記録の平均値,最頻値,中央値の大きさの関係を,不等号を用いて表したものとして,正しいものを,次のア〜力から１つ選び,記号で答えなさい。 　ア（平均値）＜(最頻値）＜（中央値） 　イ（平均値）＜(中央値）＜（最頻値） 　ウ（最頻値）＜(平均値）＜（中央値） 　エ (最頻値）＜(中央値）＜（平均値） 　オ（中央値）＜(平均値）＜（最頻値） 　力（中央値）＜(最頻値）＜（平均値）
２	＋(− )
３	a＝,b＝−1のとき, 2(4a−3b)−5a の値を求めなさい。
４	(√7＋2)(2√7−3) を計算しなさい。	８	関数y＝x2について,xの変域をa≦x≦6とすると,yの変域が10≦y≦18になりました。 　aの値を求めなさい。
５	2次方程式 x2＋5x＋3＝0 を解きなさい。	９	下の図のような,∠ABCが鈍角で,∠ACB＝36°の△ABCがあり,辺AC上に∠ADB＝73°となるように点Dをとります。また,点Cを,直線BDを対称の軸として対称移動させた点をEとします。点Eと点B,点Eと点Dをそれぞれ結ぶとき,∠BACと∠ABEの大きさの和を求めなさい。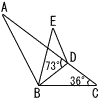
６	分速100mでx分走り,そのあと分速70mでy分歩いたところ,移動距離の合計はaｍになりました。yをa,xを使った式で表しなさい。

印刷時に改ページ

【　後　　期　】
1	−5＋14	６	2次方程式 x2−8x＋16＝0 を解きなさい。
２	−6÷32×2
３	4(x＋2y)−(−x＋y)	７	次の□に示した内容が正しくなるように,[あ],[い]のそれぞれにあてはまるものを,あとのア〜カから1つずつ選び,記号で答えなさい。 　不等式 2x＋3＜10は,「[ あ ]は,[ い ]」という数量の関係を表している。  ア　xを2倍して3を加えた数 イ　xに3を加えて2倍した数 ウ　10より大きい　　エ　10より小さい オ　10以上である　　カ　10以下である
４	等式 5a＋9b＝2 をbについて解きなさい。	８	下の図は,線分ABを直径とする円Oの円周上に,∠AOC＝90°となる点Cをとり,線分AB,BCおよび小さい方の弧CAを太い線で示したものです。BC＝4cmとするとき,太い線で囲まれた部分の面積を求めなさい。ただし,円周率をπとします。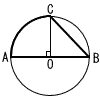
５	1 . (√6＋√24） 　√2