|
正 答 1 | |||
| 1 北海道 〜 8 茨城県 |
|
正 答 1 | |||
| 1 北海道 〜 8 茨城県 |
〜 印刷して、紙の上でやってネ! (文字サイズを小にするとA4に収まります)〜
| 1北海道 | 1 (1) 7−5=2 (2) −36+8=−28 (3) 2√3−√3=√3 2 8a+4b+a−2b=9a+2b 3 x=1のとき,y=2×1+1=3 x=4のとき,y=2×4+1=9 よって,3≦y≦9 4 最多は3人で,最頻値は25回 5 イは32+42=52, オは(√3)2+(√7)2=(√10)2だから, 直角三角形はイ・オ 6 x:(x+3)=8:12=2:3より, 3x=2(x+3)で,x=6 |
5山形県 | 1 (1) −3+8+1=6 (2) − (3) 24x2y÷(−3xy)−15xy÷(−3xy) =−8x+5 (4) (6−4√6+4)+3√6=10−√6 2 与式=(x−3y)2=( =( 3 x2+x−12−7x+8=0 x2−6x−4=0 解の公式より, x=−(−3)±√(−3)2−4×1×(−4) =3±√9+4=3±√13 4 白玉1個と赤玉1個 全6個から2個取り出す方法は, 6×5÷2=15通り 白玉2個から1個取り出す方法は,2通り 赤玉4個から1個取り出す方法は,4通り 確率=(2×4)÷15=8/15 5 △OMHで,MH=3cmより, OH2+32=92 Oh=√81−9=√72=6√2cm |
|||||||||||||||||||||||||||||||||||||
| 2青森県 | 1 ア −2 イ − エ (x2−4x+4)−(x2+3x−4)=−7x+8 オ √3−3√3−2√3=−4√3 2 2a+3b<2000 3 与式=6a3b2=6×(−2)3×(−1)2=−48 4 解の公式より,
=1−(2人ともはずれる確率) =1− 6 xL移すとすると,(42−x):(42+x)=2:5 2(42−x)=5(42+x)より,x=18 答 18L 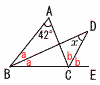 7 (右図参照) 7 (右図参照)等しい角をa,bとすると, 2a+42=2bより,a+21=b ∠x=b−a=21° 8(グラフ参照) 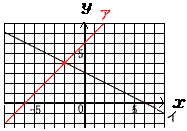 アとイの交点は アとイの交点は(−2,4) よって,x=−2,y=4 |
6宮城県 | 【前期】 1 4−14=−10 2 3 与式=8a−6b−5a=3a−6b =3× 4 14+√7−6=8+√7 5 解の公式より,
6 100x+70y=aより,70y=a−100x
7 平均値は22.1m 中央値は24・25人目の,20〜22mの階級で,21m 最頻値は10人の,18〜20mの階級で,19m よって,エ 8 a≦0の場合は,最小値が0となり,不適 x=6のときy=18だから,x=aのときy=10 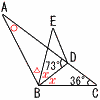 9(右図参照) △BCDで,x=73−36=37° △ABDで,∠BAC+∠ABE =180−(37+73)=70° |
|||||||||||||||||||||||||||||||||||||
| 3秋田県 | 【前期】 1 3×(−4)=−12 2 √3×2√2=2√6 3 3−4=−1℃ 4 y= y=4/xにx=2を代入して,y=4/2=2 5 上式−下式×2より,y=−3 これを下式に代入して,x−3=1より,x=4 よって,x=4,y=−3 6 (2x−1)(x+2)=0より,x= 7 与式=(x+2y)2−4(x+2y) =(x+2y){(x+2y)−4)} =(x+2y)(x+2y−4) |
6宮城県 | 【後期】
7 あ ア い エ 8 半径OB=OC=2√2 扇形OAC= △OBC= よって,面積=2π+4 cm2 |
|||||||||||||||||||||||||||||||||||||
【後期】
3 8x=6×20より,x=120÷8=15 4 両辺×2より,3x+4=8x 5x=4で,x= 5 上式×2−下式より,y=−3 これを上式に代入して,2x−9=−1で,x=4 よって,x=4,y=−3 6 (3x−2)(x−1)=0より,x=
9 6150=6.15×1000=6.15×103m 10 各辺を2乗して,N2≦n<(N+1)2 自然数nの個数は,(N+1)2−N2=2N+1=31 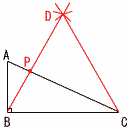 2N=30で,N=15 2N=30で,N=1511 右図 ・BCを1辺とする 正三角形BCDを作図 ・ACとBDの交点にPをとる 12 ∠A=38°より, ∠BOC=38×2=76° ∠x=(180−76)÷2=52° 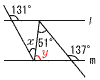 13 (右図参照) 13 (右図参照)∠y=137−51=86° ∠x=131−∠y=45° 14 底面の中心をHとすると, BD=6√2より,HD=3√2 AH2=92−(3√2)2=63で,AH=√63=3√7 よって,体積= 15 体積は底面積に比例 △APQ∽△ACDで,相似比が3:4 面積比は,32:42=9:16だから, △APQ: よって,体積は |
7福島県 | 145
5 比例定数a=xy=2×24=48
〜2番問題(おまけ)〜 1 (x−10)(x+2) 2 4a+3b>100 3 グラフ(直線の傾き)を比較して,エ 4 Bの半径をrとすると,Aの半径は2r A=π(2r)2h=4πr2h B=
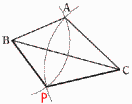 5 右図 ・BからBA=BPとなる 弧をかく ・CからCA=CPとなる 弧をかく ・2つの弧の交点をPとする |
||||||||||||||||||||||||||||||||||||||
| 4岩手県 | 1 −7 2 6a+8 3 13−6√2 4 (x−4)(x−6) 5 解の公式より,
〜2番問題(おまけ)〜 両辺を入れかえて, 両辺×3より,Sh=3V
〜3番問題(おまけ)〜 出力をx,時間をyとすると,y= これにx=500,y=240を代入して, a=500×240=120000
|
8茨城県 | 1 −2 2 −12+24=12 3 4 −4x+12y−5x−10y=−9x+2y
〜2番問題(おまけ)〜 1 (x+9)(x−4) 2 方程式にx=5を代入して, 15−4=5−2aより,a=−3 3 解の公式より,
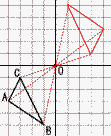 よって,(100−16)−1=83個 よって,(100−16)−1=83個5 右図 |
| [トップに戻る] [次ペ−ジに進む] |