| 1 |
 3-(-2) 3-(-2)
|
8 |
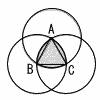
次の図のような,1辺の長さが1cmの正三角形ABCと,各頂点を中心とする半径1cmの円がある。このとき,弧AB,弧BC,弧CAで囲まれた色がついた図形の周の長さを求めなさい。
|
| 2 |
 (-63)÷9 (-63)÷9
|
| 3 |
2(3a+4b)-(2a-5b)
|
| 4 |
12ab×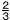 a a
|
9 |
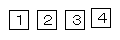 右の図のような,1,2,3,4の数字が1つずつ書かれた同じ大きさめ4枚のカードがある。この4枚のカードをよくきってから2回続けてひき,1回目にひいたカードに書かれている数を十の位とし,2回目にひいたカードに書かれている数を一の位として,2けたの整数をつくる。ただし,ひいたカードはもとにもどさない。このとき,この2けたの整数が3の倍数となる確率を求めなさい。 右の図のような,1,2,3,4の数字が1つずつ書かれた同じ大きさめ4枚のカードがある。この4枚のカードをよくきってから2回続けてひき,1回目にひいたカードに書かれている数を十の位とし,2回目にひいたカードに書かれている数を一の位として,2けたの整数をつくる。ただし,ひいたカードはもとにもどさない。このとき,この2けたの整数が3の倍数となる確率を求めなさい。
|
| 5 |
(√2+√3)2
|
|
| 6 |
方程式 x2+5x-3=0 を解きなさい。
|
|
次の度数分布表は,あるクラス20人の学習時間を整理したものである。(1),(2)を求めなさい。
| 学習時間(分) |
度数(人) |
以上 未満
0 ~30 |
1 |
| 30~60 |
2 |
| 60~90 |
7 |
| 90~120 |
6 |
| 120~150 |
2 |
| 150~180 |
2 |
| 計 |
20 |
(1) 学習時間の最頻値
(2) 学習時間の平均値
|
| 7 |
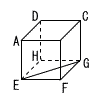 右の図のような立方体があり,線分EGは正方形EFGHの対角線である。このとき,∠AEGの大きさについて,正しく述べられている文は,ア~エのうちのどれですか,一つ答えなさい。 右の図のような立方体があり,線分EGは正方形EFGHの対角線である。このとき,∠AEGの大きさについて,正しく述べられている文は,ア~エのうちのどれですか,一つ答えなさい。
| ア |
∠AEGの大きさは,90°より大きい。 |
| イ |
∠AEGの大きさは,90°より小さい。 |
| ウ |
∠AEGの大きさは,90°である。 |
エ
|
∠AEGの大きさは,90°より大きいか小さいかは,問題の条件だけでは決まらない。 |
|
|

 右の図のような立方体があり,線分EGは正方形EFGHの対角線である。このとき,∠AEGの大きさについて,正しく述べられている文は,ア~エのうちのどれですか,一つ答えなさい。
右の図のような立方体があり,線分EGは正方形EFGHの対角線である。このとき,∠AEGの大きさについて,正しく述べられている文は,ア~エのうちのどれですか,一つ答えなさい。