全国公立高校入試 　１番問題　【平成３０年春】

（３０）和歌山県

学習日　　　 月　　 　日（　　　）

～ 印刷して、紙の上でやってネ！ （文字サイズを小にするとＡ４に収まります）～

１	(1) －9＋3	４	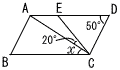右の図のように,∠ADC＝50°の平行四辺形ABCDがある。辺AD上にCD＝CEとなるように点Eをとる。 　∠ACE＝20°のとき,∠xの大きさを求めなさい。 　ただし,AB＜ADとする。
	(2)  ＋2÷(－)
	(3) －2(a－4)＋5(a－3)	５	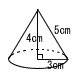右の図のように,底面の半径が3cm,高さ4cm,母線の長さが5cmの円錐すいがある。
	(4)   30. －√24  √6		(1) この円錐の体積を求めなさい。ただし,円周率はπとする。
	(5) x(x＋2y)－(x＋3y)(x－3y）
２	次の二次方程式を解きなさい。 　　(x＋3)2＝2		(2) この円錐の展開図を作図したとき,側面のおうぎ形の形として最も近いものを,次のア～エの中から1つ選び,その記号をかきなさい。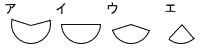
３	√60n の値が整数となるような自然数nのうち,最も小さいものを求めなさい。