全国公立高校入試
　１番問題　【平成３０年春】
正　答　４
25　滋賀県　〜　32　島根県

〜 印刷して、紙の上でやってネ！ （文字サイズを小にするとＡ４に収まります）〜

25滋賀県 １ (＋848)−(−19)＝867m
２   4＋3 a＝  7 a
 6  6
３ 上式×3＋下式より,14x＝42で,x＝3
　これを上式に代入して,2×3＋y＝11
　　よって，x＝3,y＝5
４ 与式＝3a−5a2
５ x2−8x＋15＋1＝0
　（x−4)2＝0より,x＝4
６ (1) y＝ax2に(2,6)を代入して,
　　　6＝4aより,a＝3/2
　(2) √22+62＝√4＋36＝√40＝2√10
７ √24n＝2√6nより,n＝6
８ Ｂ÷Ａ＝(πr2×2r)÷(  4 πr3÷2)
 3
　＝ 2πr3×3 ＝ 3杯分
2πr3
９ 2回の引き方は,5×4＝20通り
　素数は，13,23,31,41,43,53の6通り
　よって，確率＝  6 ＝  3
20 10
28兵庫県
１ 4−6＝−2　　２   5−8 ＝−  3
 10 10

３ 4√7−2√7＝2√7

４ 解の公式より，
　x＝ −3±√32−4×1×1
2×1
　　＝ −3±√5
2

５ y＝  a に(−4,6)を代入して,
 x
　 6＝  a より,a＝−24で,y＝− 24
−4  x
　これにx＝3を代入して,y＝− 24 ＝−8
 3

６ ∠x＝360−110×2＝140°

７ イ
26京都府 　【前期】
１ −4＋  8 ＝− 12
 5  5
２   4a2b×5×7b2 ＝−70ab2
−2ab
３ (4x2−4x＋1)−(x2−3x−18)
　＝3x2−x＋19
４ 外角の和は360°だから,
　180−360÷30＝180−12＝168°
５ 上式×3−下式×4より,
　7x＝35で,x＝5
　これを下式に代入して,
　　2×5＋3y＝−2で,y＝−4
　よって,x＝5,y＝−4

６ 与式＝xy(x−2)＝(6−4)√6＝2√6

７ (3x−5)(x＋1)＝0より,x＝5/3,-1

８ 一次関数では,変化の割合＝傾きだから,
 yの増加量 ＝  4 で,yの増加量＝4×6÷3＝8
　6  3
９ 中央値は(5+x)/2だから,
　平均値＝ 2+2+5+x+13+15 ＝ 5＋x で, x＝11
6 2 
29奈良県 １ (1) 3＋5＝8　　(2) 4×9＝36
　(3)   12a2b2×2 ＝−4
 −6ab×ab
　(4) （x2＋9x＋20)−(x2−9)＝9x＋29
２ 解の公式より，
　x＝ −5±√52−4×2×1
2×2
　　＝ −5±√17
4
３ ア
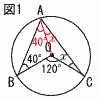
４ (右図参照)
　∠Ａ＝∠x＋40＝60より,
　　∠x＝20°
５ 各辺を2乗して，25＜a＜36
　a＝26,27,…,35で，自然数は10個
６ 560＝24×5×7＝2×23×5×7より,
　4つの数は2，5，7，8
７ 1−(5以上の目が出ない確率)
　確率＝1− 4×4 ＝1−  4 ＝  5
6×6  9  9
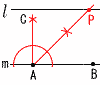８ ウ
９ 右図
　・mの垂線ＡＣを引く
　・∠BACの二等分線との
　　　交点をPとする
　【中期】

１ −8＋5＝−3
２ 3x＋15y−14x＋12y＝−11x＋27y
３ 3√7＋ 　2√7 . −2√7＝√7＋ 2√7 ＝  9 √7
√7√7 7  7
４ a(x2−12x＋27)＝a(x−3)(x−9)
５ x2−16＝−1より,x2＝15で,x＝±√15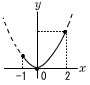
６ (右図参照)
　x＝2のとき,y＝(3/2)×22＝6
　　よって,0≦y≦6
７ 総得点は
　　1･5+2･6+3･4+4･3+5･2＝51点
　2点は6試合だから,12÷51≒0.24
８ ∠ＡＣＢ＝34°より,∠Ａ＝180-34×2＝112°
　∠x＝360−112×2＝136°		 30和歌山県
１ (1) −6　(2)　  1 − 2×5 ＝−  4 ＝−2
 2 4  2
　(3) −2a＋8＋5a−15＝3a−7
　(4)   30√6 −2√6＝5√6−2√6＝3√6
 6
　(5) (x2＋2xy)−(x2−9y2)＝2xy＋9y2
２ x＋3＝±√2より,x＝−3±√2
３ √60n＝2√15nより,n＝15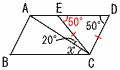
４ (右図参照)
　∠DEC＝∠BCE(錯角)で
　∠x＝50−20＝30°
５
(1) 32π×4÷3＝12πcm3
(2) 底面(円)の円周＝6π
　　側面(扇形)の弧＝10π×（3/5）
　(3/5)の形から，ア
27大阪府 　【A問題】
１ 7＋1＝8　　２ −7.2
３ 4/9　　４ 8x−5y
５ 6x
６ 6√7−2√7＝4√7

　〜２番問題（おまけ）〜
１ 15.0−(−3.5)＝18.5℃
２ −3×(−9)＋4＝27＋4＝31
３ 2x＝18より,x＝9

　【B問題】
１ −2−9＝−11

２ 9a−4b−8a＋2b＝a−2b

３ 3＋4√3＋4＝7＋4√3

４ (x−9)(x＋3)＝0より,x＝9,−3

５ 2nは偶数だから,2n＋1は奇数で，ウ

６ √34.52＜√21＜√34.62より,
　4.5＜√21＜4.6で，小数第1位は5

７ 日〜水は,(6.0+3.9+4.1+4.8)÷4＝4.7
　(7.4+6.6+x)÷3＝4.7＋2.4で,
　　x＝7.1×3−14＝7.3

８ 6枚から同時に2枚取り出す方法は，
　　　6×5÷2＝15通り
　2個…(a,b)＝(1,4) (2,5) (3,6)
　3個…(a,b)＝(1,5) (2,6)
　4個…(a,b)＝(1,6)
　よって,確率＝ 3＋2＋1 ＝  6 ＝  2
15 15  5

９ y＝ax2にx＝−5を代入して,Ｂ(−5,25a)
　よって,Ｃ(5,25a)　　また,Ａ(−5,0)で,
　l の傾き＝ 25a−0 ＝ 25a ＝  3
5−(−5) 10  5
　a＝  3 ×  2 ＝  6
 5  5 25
31鳥取県 １ (1) 2　 (2) −1/6　 (3) √3
　(4) 14x−6　 (5) 3ab2
２ h(a＋b)＝2Ｓより,b＝ 2Ｓ −a
h
３ (a＋5)(a−3)
４ 解の公式より，
　x＝ −(−5)±√(−5)2−4×3×1
2×3
　　＝ 5±√13
6
５ (右図参照)
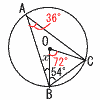
　∠ＢＯＣ＝72°∠ＢＡＣ＝36°
　36＋2x＋54×2＝180より,
　　∠x＝(180−144)÷2＝18°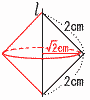
６ エ　(y＝12/x)
７ （右図参照) 円すい2個
　円すいの半径,高さは√2cm
体積＝(√2)2π×√2÷3×2
　＝ 4√2 πcm3
3
８ 素数の目は2,3,5で,確率＝  9 ＝  1
36  4
９ 4本で1個，3本増えるごとに1個追加
　(100−4)÷3＝32で,1＋32＝33個
10　
　AC＝GE(仮定)…ア
　AD//FGより,∠BAC＝∠FGE(錯角)…イ
　BC//DFより,∠ACB＝∠AED(同位角)
　　∠AED＝∠GEF(対頂角)だから，
　　∠ACB＝∠GEF…ウ
　アイウより,1組の辺とその間の角が
　　等しいから,△ABC≡△GFE
32島根県 １ 10　 ２ ±4　 ３ 11x−13y　 ４ x＝2,−8
５ ウ　 ６ 5x＝3(x＋4)で,x＝6より,−1/2
  ア イ ウ エ
最頻値  5  2  6  5
中央値  5  4  6  6
７ イ,エ
８ 高さ＝√42−22＝2√3cm
 1 ×42×2√3＝ 32√3 cm3
 3 3
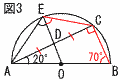９ (右図参照)
　∠B＝70°より,
　　∠AEC＝110°
　∠OEA＝110÷2−55°
［トップに戻る］　［前ページに戻る］　［次ペ−ジに進む］