全国公立高校入試 　１番問題　【平成３０年春】

（２４）三重県

学習日　　　 月　　 　日（　　　）

〜 印刷して、紙の上でやってネ！ （文字サイズを小にするとＡ４に収まります）〜

【　前　　期　】
1	−9−2×4	７	一の位の数が4である2けたの自然数Aが,Aの各位の数の和の7倍に等しいとき,自然数Aを求めなさい。
２	(6xy−27y2)÷(−y)
３	x＝3,y＝−7のとき,5(x＋2y)−4(2x＋3y) の値を求めなさい。	８	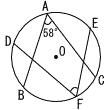右の図のように,3点A,B,Cは円Oの周上にあり,∠BAC＝58°である。点Cをふくまない側にあるAB上に,AD＝DB となるように点Dをとり,点Bをふくまない側にあるCA上に,CE＝EAとなるように点Eをとる。点Aをふくまない側にあるBC上に点Fをとるとき,∠DFEの大きさを求めなさい。
４	一次関数 y＝x＋1 について,xの増加量が5のときのyの増加量を求めなさい。
５	8 − √54 3 4	９	次の図で,△ABCの∠ABCの二等分線上にある点Dと,頂点B,Cを結んでできる三角形のうち,△DBC＝△ABCとなる△DBCを,定規とコンパスを用いて作図しなさい。 　なお,作図に用いた線は消さずに残しておきなさい。
６	二次方程式 (2x−1)2＝3(x−1)(x＋2)＋25 を解きなさい。

印刷時に改ページ

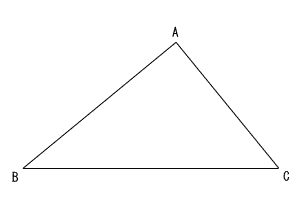【　後　　期　】
1	−16＋11	６	二次方程式 3x2−x−1＝0 を解きなさい。
２	−12x÷(−3)
３	x＋y − 3x−5y  　2 8	７	階級(m) 度数(人) 以上 未満 10〜15  2 10〜15 8 15〜20 11 20〜25 13 25〜30 5 30〜35 1 計 40 　右の表は,ある中学校の3年生40人のハンドボール投げの記録を度数分布表に整理したものである。この度数分布表について,次の各問いに答えなさい。
４	（√3−2√5)2		(1) 最頻値を求めなさい。
５	6x2−24 を因数分解しなさい。		(2) 10m以上15m未満の階級の相対度数を求めなさい。