全国公立高校入試 　１番問題　【平成３０年春】

（２３）愛知県

学習日　　　 月　　 　日（　　　）

〜 印刷して、紙の上でやってネ！ （文字サイズを小にするとＡ４に収まります）〜

【　　Ａ　　】
1	6−(−24)÷6	７	ある中学校の生徒数は180人である。このうち,男子の16％と女子の20％の生徒が自転車で通学しており,自転車で通学している男子と女子の人数は等しい。 　このとき,自転車で通学している生徒は全部で何人か,求めなさい。
２	7x−4 − x−1  8 2
３	3 . ＋ √20 　√5 5	８	世帯数が60000世帯のＡ市で,300世帯を無作為に抽出してテレビで番組Ｔを視聴していた世帯数を調査したところ,45世帯が視聴していた。 　このとき,Ａ市全体でこの番組Ｔを視聴していた世帯はおよそ何世帯と推定されるか,求めなさい。
４	(2x−3)(x＋2)−(x−2)(x＋3)
５	方程式 (x＋6)(x−2)＋2＝7x を解きなさい。	９	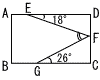図で,四角形ABCDは長方形,E,F,Gはそれぞれ辺AD,DC,BC上の点である。 　∠DEF＝18° ∠FGC＝26°のとき,∠EFGの大きさは何度か,求めなさい。
６	nは自然数で,√24n がある自然数になる。このようなnのうちで最も小さい数を求めなさい。

印刷時に改ページ

【　　Ｂ　　】
１	2×(−3)＋10	７	関数 y＝ax2（aは定数）と y＝3xについて,xの値が1から3まで増加するときの変化の割合が同じであるとき,aの値を求めなさい。
２	6ab×(−3ab)2÷27ab2
３	(√3＋1)2−2(√3＋1)	８	赤玉3個,白玉2個,青玉1個が入っている箱がある。この箱から玉を同時に2個取り出すとき,同じ色の玉を取り出す確率を求めなさい。
４	(x＋1)(x＋4)−2(2x＋3) を因数分解しなさい。
５	方程式 x(x＋1)＝2(1−x) を解きなさい。	９	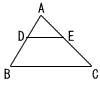図で,D,Eはそれぞれ△ABCの辺AB,AC上の点で,DE//BCである。 　AD＝2cm,BC＝10cm,DE＝4cmのとき,線分DBの長さは何cmか,求めなさい。
６	クラスで記念作品をつくるために１人700円ずつ集めた。予定では全体で500円余る見込みであったが,見込みよりも7500円多く費用がかかった。そのため,１人200円ずつ追加して集めたところ,かかった費用を集めたお金でちょうどまかなうことができた。 　記念作品をつくるためにかかった費用は何円か,求めなさい。