全国公立高校入試 　１番問題　【平成３０年春】

（１０）群馬県

学習日　　　 月　　 　日（　　　）

〜 印刷して、紙の上でやってネ！ （文字サイズを小にするとＡ４に収まります）〜

【　前　　期　　】
1　　番　　問　　題		２　番　問　題　（おまけ）
1	(1) 5−(−3)	１	2次方程式 (x−3)2＝2 を解きなさい。
	(2) 6−5×(−2)
	(3) 4x−7x	２	yはxに比例し,x＝3のとき,y＝−15である。yをxの式で表しなさい。
	(4) (2x＋7y)−4(x−y）
	(5) 18a3÷a	３	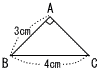右の図の直角三角形ABCにおいて,辺ACの長さを求めなさい。
	(6) √75−√27
２	(2x＋3)(2x−3) を展開しなさい。	４	大小2個のさいころを同時に投げるとき,出た目の和が8となる確率を求めなさい。
３	x2＋6x＋8 を因数分解しなさい。

印刷時に改ページ

【　後　　期　】
１	(1) 3＋4×(−2）	６	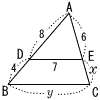右の図において,DE//BCであるとき,x,yの値をそれぞれ求めなさい。
	(2) 6x2y÷2xy
	(3) a− a−3 2	７	2次方程式 x2＋2x＝1 を解きなさい。
２	8の平方根を求めなさい。
３	x＝2,y＝−3のとき，2(x−3y)−(3x−5y) の値を求めなさい。	８	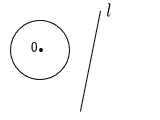右の図のように,円Oと直線がある。円Oの周上にある点で,直線ｌまでの距離が最も短くなるような点Ｐを,コンパスと定規を用いて作図しなさい。 　ただし,作図に用いた線は消さないこと。
４	(a−4)2＋4(a−4)−12 を因数分解しなさい。
５	直線y＝−3x＋2に平行で,点(1,−4)を通る直線の式を求めなさい。	９	十の位の数と一の位の数の和が10である2けたの自然数がある。この自然数の十の位の数と,一の位の数を入れかえた自然数は,もとの自然数より36大きくなる。もとの自然数を求めなさい。