| 1 |
(1)  3+(-7) 3+(-7)
|
7 |
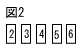 図2のような5枚のカードをよくきって,続けて2枚引く。引いたカードの1枚目の数字を十の位,2枚目の数字を一の位として2けたの整数をつくる。この整数が偶数となる確率を求めなさい。 図2のような5枚のカードをよくきって,続けて2枚引く。引いたカードの1枚目の数字を十の位,2枚目の数字を一の位として2けたの整数をつくる。この整数が偶数となる確率を求めなさい。
|
| (2) |
 |
(- |
2 |
)÷ |
4 |
| 9 |
3 |
|
(3)  √18-√8 √18-√8
|
8 |
「連続する3つの整数の和は,3の倍数になる」ことを,次のように説明した。
このとき,[ア],[イ],[ウ]にあてはまる式を答えなさい。
連続する3つの整数のうち,最も小さい整数をnとすると,残りの2数は小さい方から[ア],[イ]と表すことができる。この3つの連続する整数の和は,
n+[ア]+[イ]=3n+3=[ウ]
[ア]は整数だから,[ウ]は3の倍数である。
つまり,連続する3つの整数の和は,3の倍数になる。 |
|
(4) 3(2x+y)-(x-4y)
|
(5) 12a3b÷(-3a2)×2ab
|
| 2 |
| 等式 S= |
1 |
ah をhについて解きなさい。 |
| 2 |
|
9 |
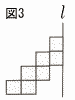  図3のように,一辺の長さが2cmの正方形を7枚組み合わせた図形がある。この図形を,直線l を回転の軸として1回転させてできる回転体の体積を求めなさい。 図3のように,一辺の長さが2cmの正方形を7枚組み合わせた図形がある。この図形を,直線l を回転の軸として1回転させてできる回転体の体積を求めなさい。
|
| 3 |
4x2-81 を因数分解しなさい。
|
| 4 |
二次方程式 x2+3x-1=0 を解きなさい。
|
10 |
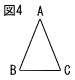 図4のような二等辺三角形ABCにおいて,「AB=ACならば,∠B=∠Cである」ことを,次のように証明した。空欄に証明の続きをかき,証明を完成しなさい。 図4のような二等辺三角形ABCにおいて,「AB=ACならば,∠B=∠Cである」ことを,次のように証明した。空欄に証明の続きをかき,証明を完成しなさい。
(証明)
点Aから辺BCに垂線をひき,辺BCとの交点をDとする。
△ABDと△ACDで,
合同な図形では,対応する角は等しいので,
∠B=∠C (証明終)
|
| 5 |
まで変わるときの変化の割合を求めなさい。
|
| 6 |
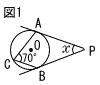 図1において,∠xの大きさを求めなさい。ただし,PA,PBは円Oの接線で,点A,Bはその接点である。また,点Cは円Oの周上の点である。 図1において,∠xの大きさを求めなさい。ただし,PA,PBは円Oの接線で,点A,Bはその接点である。また,点Cは円Oの周上の点である。
|
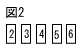 図2のような5枚のカードをよくきって,続けて2枚引く。引いたカードの1枚目の数字を十の位,2枚目の数字を一の位として2けたの整数をつくる。この整数が偶数となる確率を求めなさい。
図2のような5枚のカードをよくきって,続けて2枚引く。引いたカードの1枚目の数字を十の位,2枚目の数字を一の位として2けたの整数をつくる。この整数が偶数となる確率を求めなさい。
 図4のような二等辺三角形ABCにおいて,「AB=ACならば,∠B=∠Cである」ことを,次のように証明した。空欄に証明の続きをかき,証明を完成しなさい。
図4のような二等辺三角形ABCにおいて,「AB=ACならば,∠B=∠Cである」ことを,次のように証明した。空欄に証明の続きをかき,証明を完成しなさい。 図1において,∠xの大きさを求めなさい。ただし,PA,PBは円Oの接線で,点A,Bはその接点である。また,点Cは円Oの周上の点である。
図1において,∠xの大きさを求めなさい。ただし,PA,PBは円Oの接線で,点A,Bはその接点である。また,点Cは円Oの周上の点である。