全国公立高校入試
　１番問題　【平成２９年春】
正　答　４
25　滋賀県　〜　32　島根県

〜 印刷して、紙の上でやってネ！ （文字サイズを小にするとＡ４に収まります）〜

25滋賀県 １ −1−2＝−3℃
２   2a−6a＋15a ＝ 11 a
 6  6
３ 下式−上式×3より，
　11y＝−11で，y＝−1
　これを上式に代入して，
　　x−5×(−1)＝4で，x＝−1
　よって，x＝−1,y＝−1
４   8√2 −5√2＝4√2−5√2＝−√2
 √2√2
５   8a2b×2 ＝16a
 ab
６ (x＋6)(x−3)＝0より，x＝−6,3
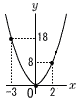７（右図参照）
　x＝−6のとき，y＝2×(−3)2＝18
　x＝0のとき，y＝2×02＝0
　x＝2のとき，y＝2×22＝8
　よって，0≦y≦18
８ 40:x＝23:33
　8x＝40×27より，x＝13.5cm3
段  1  2  3  4  5
枚  2  7  15  26  40
増加  +5  +8  +11  +14  
９（右表参照）
　1段の高さは，
　　√92−32
　　　＝6√2
　よって，6√2×5＝30√2cm		 28兵庫県 １ −6
２   8-15 ＝−  3
 20 20
３ 3√6−2√6＝√6
４ 解の公式より，
　x＝ −1±√12−4×1×(−3)
2×1
　＝ −1±√1＋12 ＝ −1±√13
2 2
５ y＝− 12 に，(a,2)を代入して，
 x
　2＝− 12 より，a＝− 12 ＝−6
 a  2
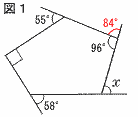６（右図参照）
　外角の和は360°で，
　∠x＝360−(84＋55
　　＋90＋58)
　 ＝360−287＝73°
７
　平均値＝（4×3＋6×4
　 ＋7×6＋8×10＋9×12＋10×5)÷40
　 ＝(12＋24＋42＋80+108＋50）÷40
　 ＝316÷40＝7.9点
　中央値(20･21人目)＝8点
　最頻値（12人）＝9点
　よって，ア　　
26京都府 　【前期】

１  27×8 − (−12)×(−5)
4×(−3) 2 
　＝−18−30＝−48
２   5(5a−2b)−8(3a−4b) ＝ a＋22b
 8×5 40
３   5√2 − 　10√3 ＋ 2√3
 √2√3 √3√3 √√3
　＝  5 √3− 10 √3＋  2 √3＝−√3
 3  3  3
４ 6:16＝4.5:xより，
　x＝ 16×4.5 ＝12km 
6
５ y＝  a に(2,−9)を代入して， 
 x
　−9＝  a より，a＝−18（比例定数）
 2
　式 y＝− 18 にx＝−6を代入して，y＝3
x
６ 連立方程式を2つに分けて，
 {  4x−3y＝19
 6x−2y＝21
　下式×3−上式より，
　　10x＝25で，x＝5/2
　これを上式に代入して，
　　4×(5/2)−3y＝19で，y＝−3
　よって，x＝  5 ，y＝−3
 2
７ 2x2−9x＋10＝x2−2x＋1＋4
　x2−7x＋5＝0
　解の公式より，
　x＝ −(−7)±√(−7) 2−4×1×5
2×1  
　＝ 7±√49−20 ＝ 7±√29
2 2
８ 三平方の定理より，
　√122−82＝√144−64＝√80＝4√5cm
９ 平均値＝(3×6＋9×10＋15×14
　　　＋21×8＋27×2)÷40＝13.5m
　最頻値＝15m


　		 29奈良県 １ (1) −14　　（2） −9×5＝−45
　 (3)   4a2b2×3a ＝2ab
 6a2b
　 (4) x2＋6x＋9−2x−6＝x2＋4x＋3
２ 次のような連立方程式に分ける
 {  2x＋y＝x−5y−4  …ア
 2x＋y＝3x−y  …イ
　アより，x＋6y＝−4 …ア'
　イより，−x＋2y＝0 …イ'
　ア’＋イ'より，8y＝−4で，y＝−1/2
　これをア'に代入して，
　　x−3＝−4で，x＝−1
　よって，x＝−1,y＝−  1
 2
３ (x＋6)(x−1)＝0より，x＝−6,1
４ 与式＝(x＋y)2−3xy
　　＝(2√5)2−3×(5−4)
　　＝20−3＝17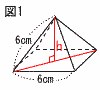
５（右図参照）
　底面の対角線は6√2cm
　高さをhとすると，
　 h2＋(3√2)2＝62
　 h2＋18＝36で，h＝3√2
　体積＝  1 ×62×3√2＝36√2cm3
 3
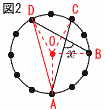６（右図参照）
　∠AOB＝90°より，
　 ∠ADB＝45°…ア
　∠COD＝60°より，
　 ∠CAD＝30°…イ
　ア＋イより，
　 ∠x＝45＋30＝75°
７ 玉の総数をx個とすると，
　30:x＝6:30で，x＝30×30÷6＝150
　よって，およそ150個
８ 次の4通り考えられるから，
6√5
  6√5   6√5   6√5
√5   ， 2√5  ， 3√5  ， 6√5
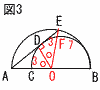　よって，n＝5,20,45,180
９（右図参照）
　△ＯＡＥは二等辺三角形
　ＯＤ⊥ＡＥより，
　 ∠ＡＯＤ＝∠ＥＯＤだから，
　　弧ＣＤ＝弧ＤＦ　よって，6:7
　【中期】
１　−8−36＝−44
２   5(46a−3b)−4(35a−2b) ＝ 90a−7b
 2×5 10
　または，9a−  7 b
10
３ 3√2＋2√2＝5√2
４ 上式×2＋下式×3より，
　17x＝−34で，x＝−2
　これを上式に代入して，
　　4×(−2)＋3y＝1で，y＝3
　よって，x＝−2,y＝3
５ x＋6＝Ａとすると，
　与式＝Ａ2−13Ａ＋40＝(Ａ−5)(Ａ−8)
　　＝(x＋6−5)(x＋6−8)＝(x＋1)(x−2)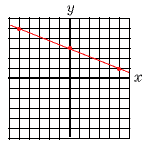
６ 解は右図
　グラフは切片3，
　　傾き−2/5の直線
７ 解の公式より，
　x＝ 5±√25＋16
8
　 ＝ 5±√41 
8
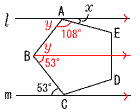８（右図参照）
　∠Ａ＝∠Ｂ＝108°
　y＝108−53＝55°
∠x＝180−55−108
　　＝17°
 30和歌山県
１ (1) −3　(2) 2−  1 ＝  3
 2  2
　(3) 4a＋5b−2a＋6b＝2a＋11b
　(4) 2√2＋ 　6√2 . ＝2√2＋3√2＝5√2
√2√2
　(5) 4a2＋4a＋1−a2＋9＝3a2＋4a＋10

２ 2ab(3a−2b＋4)

３
　√9＜√10＜√16より，√10＝3.***
　√36＜√38＜√45より，√38＝6.***
　3.***＜n＜6.***だから，
　　n＝4,5,6で，3個

４ y＝  a に (4,-9)を代入して，
 x
　−9＝  a で，a＝-36（比例定数）
 4
　よって，y＝− 36
 x

５
(1) 平均値＝(10×2＋11×5±12×8
　　　＋13×12＋14×3)÷30
　　＝(20＋55＋96＋156＋42)÷30
　　＝369÷30＝12.3度
(2) 1500× 15 ＝750個
30
27大阪府 　【Ａ問題】

１ −4

２ 1.2＋2.3＝3.5

３ −12

４ 2x＋4y

５ 9x2

６ 5√2＋2√2＝7√2




　〜２番問題（おまけ）〜


１ √10＜√16より，0＜√10＜4
　よって，1,2,3

２ −5×2＋4＝−10＋4＝−6

３ x2＋5x−24

４ 上式−下式より，
　2x＝6で，x＝3
　これを下式に代入して，
　　3＋2y＝1で，y＝−1
　よって，x＝3,y＝−1

５ (2,6) (3,4) (4,3) (6,2)の4通りで，
　確率＝ 　4　. ＝  4 ＝  1
6×6 36  9



　		 31鳥取県
１ (1) 3−7＝−4　　(2) 　−2×3 ＝−  1
　9×4  6
　(3) 3√2−2√2＝√2
　(4) 6x＋3y−x＋4y＝5x＋7y
　(5)  　12a3×2ab ＝−8a2b2
 　−3a2
２ まず両辺を入れ替える
　1 ah＝Ｓで，h＝ 2Ｓ
　2 a 
３ (2x＋9)(2x−9)
４ 解の公式より，
　x＝ −3±√32−4×1×(−1)
2×1
　 ＝ −3±√13 
2
５ x,yの増加量を計算
xの増加量＝3−1＝2
yの増加量   6 −  6 ＝2−6＝−4
 3  1
　よって，変化の割合＝−4÷2＝−2
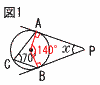６（右図参照）
　∠ＡＣＢ＝70×2＝140°
四角形ＡＣＢＰで，
　∠x＝360−140−90×2
　　＝40°
７ 引き方は全部で，5×4＝20通り
　このうち偶数は，一位が3通り，
　　十位は残りで4通りで，3×4＝12通り
よって，確率＝ 12 ＝  3
20  5
８ ｱ n＋1，ｲ n＋2，ｳ 3(n＋1)
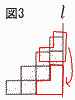９（右図参照）
・上2段を下へ移して考える
　62π×2＋82π×2＝200πcm3
10
・∠ADB＝∠ADC＝90°(作図)
・AB＝AC(仮定，等辺)
・AD＝AD(共通)
　直角三角形の斜辺と他の1辺がそれぞれ
　　等しいから，△ABD≡△ACD
　【Ｂ問題】
１ −15＋10＝−5
２   4ab2×9a2 ＝3ab
 4×3a2b
３ 1−2√2＋2＋ 　6√2 . ＝3−2√2＋3√2
√2√2
　＝3＋√2
４ 2x2−2x＋3x−3−x2−5x
　＝x2−4x−3
５ 3b＝2a＋7より，2a＝7−3b
　a＝ 7−3b または，a＝−  3 b＋  7
2  2  2
６ ア 範囲＝32.5−12.5＝20m
　イ 中央値(10と11番目)＝17.5m
　ウ 相対度数＝3÷20＝0.15
　エ 最頻値(7人)＝17.5m
　よって，ウ
７ b/a＝1/1,2/1,3/1,4/1,5/1,6/1,2/2,
　　4/2,6/2,3/3,6/3,4/4,5/5,6/6の14通り
　よって，確率＝ 14 ＝  7
36 18
８ Ａ(2,3) Ｃ(2,0)だから，ＡＣ＝3で，
　これを底辺と考えると，高さは10/3
　Ｂ,Ｄのx座標は，2−10/3＝−4/3で，
　Ｂ(− 4 ， 4 )，Ｄ(− 4 ， 16 a）
3 3 3 9
よって，ＢＤ＝ 4 − 16 a＝3
3 9
　12−16a＝27で，a＝− 15
16
32島根県
１   9×(−2） ＝ −18 ＝3
 −6 −6 

２ 3√2＋5√2−3･2√2＝2√2

３ 3b＝6c−2a
　b＝ 6c−2a または，b＝−  2 a＋2c
3  3

４ 解の公式より，
　x＝ −5±√25＋16
2
　 ＝ −5±√41 
2

５ y＝axに (12,−8)を代入して，
　−8＝12aで，a＝ −8 ＝−  2 （比例定数）
12  3
　式y＝− 2 xに x＝−3を代入して，y＝2
3

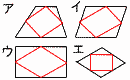６（右図参照）　イ

７（右図参照）
　h＝√52−32＝4cm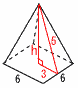
　体積＝  1 ×62×4＝48cm2
 3

８ イ,ウ
　
［トップに戻る］　［前ページに戻る］　［次ペ−ジに進む］