| 【 Ｂ 問 題 】 |
| １ |
 5×(−3)−20÷(−2)
|
６ |
ハンドボール
投げの記録(m) |
度数
(人) |
以上 未満
10〜15 |
4 |
| 15〜20 |
7 |
| 20〜25 |
5 |
| 25〜30 |
3 |
| 30〜35 |
1 |
| 合 計 |
20 |
右の表は，生徒20人のハンドボール投げの記録を度数分布表にまとめたものである。次のア〜エのうち，この度数分布表からわかることとして正しいものはどれですか。一つ選び，記号を○で囲みなさい。
| ア |
生徒20人の記録の範囲は25m以上である。 |
イ
|
生徒20人の記録の中央値は20m以上25m未満の階級にふくまれている。 |
ウ
|
25m以上30m未満の階級の相対度数は0.15である。 |
| エ |
度数が最も多い階級の階級値は32.5mである。 |
|
| ２ |
| 4ab2×(− |
3a |
)2÷3a2b |
 |
| 2 |
|
| ３ |
|
７ |
Ａ,Ｂ二つのさいころを同時に投げ，Ａのさいころの出る目の数をa，Ｂのさいころの出る目の数をbとするとき，b/aが整数である確率はいくらですか。1から6までのどの目が出ることも同様に確からしいものとして答えなさい。
|
| ４ |
(2x＋3)(x−1)−x(x＋5）
|
８ |
 |
右図において，mは y＝ |
3 |
x2 のグラフを |
 |
| 4 |
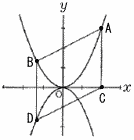 表し，nは y＝ax2(a＜0) のグラフを表す。Ａ,Ｂはm上の点であって，Ａのx座標は2であり，Ｂのx座標は負である。Ｃはx軸上の点であり，Ｃのx座標はＡのx座標と等しい。Ｄはn上の点であり，Ｄのx座標はＢのx座標と等しい。4点Ａ,Ｂ,Ｄ,Ｃを結んでできる四角形ＡＢＤＣは平行四辺形である。平行四辺形ＡＢＤＣの面積が10cm2であるときのaの値を求めなさい。求め方も書くこと。ただし，座標軸の1目もりの長さは1cmであるとする。
|
| ５ |
| 等式 b＝ |
2a＋7 |
をaについて解きなさい。 |
 |
| 3 |
|
