| １ |
(1)  −6＋11
|
７ |
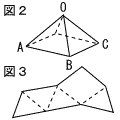  図2のように，点０，Ａ，Ｂ，Ｃ，Ｄを頂点とし，全ての辺の長さが等しい正四角すいがある。図3はこの正四角すいの展開図の1つである。図3の展開図をつくるためには，図2の正四角すいの3辺ＯＡ，０Ｂ，ＢＣに加えて，どの1辺を切り開けばよいか。
次のア〜オから1つ選び，その記号を書け。
ア 辺ＯＣ イ 辺ＯＤ ウ 辺ＡＢ
エ 辺ＡＤ オ 辺ＣＤ
|
(2) −42÷2
|
(3) 3ab2×4a2÷(−6ab)
|
(4) (x＋y)(x−3y）＋2xy
|
| ２ |
2次方程式 x2−12x＋36＝0 を解け。
|
８ |
2つのさいころＡ，Ｂを同時に1回投げて，Ａのさいころの出た目の数をa，Ｂのさいころの出た目の数をbとする。
このとき，「（ ）になる確率は1/12である」 が成り立つように，（ ）に当てはまる等式を1つ，a，bを用いて表せ。
|
| ３ |
3＜√7a＜5 を満たす自然数aを全て求めよ。
|
| ４ |
半径が6cm，中心角が80°のおうぎ形の面積を求めよ。ただし，円周率はπとする。
|
９ |
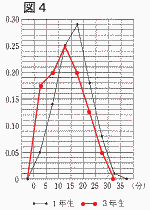 ある中学校の1年生100人と3年生120人に通学時間についてアンケートをした。図4は，その結果について，各階級の相対度数を折れ線グラフに表したもので，縦軸は相対度数を表している。
例えば，1年生の5分以上10分未満の階級の相対度数は0．14である。
図4から読み取ることができることがらとして適切なものを，次のア〜オから全て選び，その記号を書け。
ア
|
通学時間の最大値は，１年生の方が３年生より大きい。 |
イ
|
通学時聞か20分以上25分未満の階級の相対度数は，1年生の方が3年生より小さい。 |
ウ
|
通学時間が10分未満の生徒の人数は，1年生の方が3年生より多い。 |
エ
|
通学時間が10分以上15分未満の生徒の人数は，1年生の方が3年生より少ない。 |
オ
|
全体の傾向としては，1年生の方が3年生より通学時間が長いといえる。 |
|
| ５ |
関数ｙ＝ax2 のグラフの特徴として適切なものを，次のア〜オから全て選び，その記号を書け。
| ア |
原点を通る。 |
| イ |
x軸について対称な曲線である。 |
| ウ |
a＞0のときは上に開き，x軸より下側にはない。 |
エ
|
a＜0のとき，xの値が増加すると，x＞0の範囲では，yの値は減少する。 |
オ
|
aの値の絶対値が大きいほど，グラフの開き方は大きい。 |
|
| ６ |
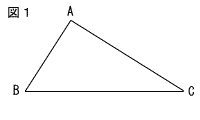 図１の△ＡＢＣにおいて，辺ＢＣ上にあって，辺ＡＢと辺ＡＣまでの距離が等しい点をＰとする。点Ｐを，定規とコンパスを使って解答欄の枠内に作図せよ。なお，作図に使った線は消さずに残しておくこと。
|
